Matrices, récurrence

par **juju78** » 10 Mar 2009, 10:22

Bonjour!

Soit

Et I la matrice idendité de M3(R)
On me demande de calculer B² =

On me demande de montrer par récurrence que, pour tout

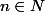
et

B

Mais je ne vois pas comment faire?

par **fatal_error** » 10 Mar 2009, 10:33

salut,

ben si

On suppose

on look n+1 :

Pour le cas

:

par **juju78** » 10 Mar 2009, 23:30

Ok j'ai compris pour

Mais pour B^{2n+1} je n'ai pas compris

Or ou est passé le I ? c'est parce que 'lon sait que A.I= A ? on peut l'enlever?

par **Nightmare** » 10 Mar 2009, 23:33

Salut :happy3:

L'identité dans Mn(K) a le même rôle neutre que l'unité dans R.

Si B était un nombre réel, on aurait bien

non?

par **juju78** » 10 Mar 2009, 23:57

Exact, merci:)

On considère ensuite les deux suites (Xn) et (Yn) définies par

X0=1, Y0=2 et

X(n+1)= Xn + 2Yn
Y(n+1)=2Xn - Yn

On pose

On me demande alors quelle relation matricielle relie V(n+1) et Vn

Mais je ne vois pas trop?

par **Nightmare** » 11 Mar 2009, 00:02

Tout est écrit dans la définition récurrente de tes suites :

ie :

par **juju78** » 11 Mar 2009, 08:25

Mais comment sait on que :

(je n'ai pas encore commencé le cour la dessus , je m'avance un peu dans les exos mais j'aimrais comprendre avant)

par **SimonB** » 11 Mar 2009, 09:36

Par définition du produit matriciel...

par **juju78** » 11 Mar 2009, 16:51

a ui j'ai compris !

On me demande ensuite quelle est l'expression de Vn en fonction de B,n et Vo

Mais la je ne vois pas ;s

par **Nightmare** » 11 Mar 2009, 16:52

La suite V(n) est géométrique, conclus.

par **juju78** » 11 Mar 2009, 18:00

A oui!
donc

par **Nightmare** » 11 Mar 2009, 18:02

C'est bien ça. :happy3:

par **juju78** » 11 Mar 2009, 18:46

Par contre (dsl) dans une derniere question on me demande de determiner Xn et Yn en fonction de n, X0 et Y0

mais la pareil je bloque