Matrice et récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
log86
- Membre Relatif
- Messages: 169
- Enregistré le: 25 Nov 2007, 14:17
-
 par log86 » 09 Mai 2008, 07:54
par log86 » 09 Mai 2008, 07:54
Bonjour j'ai un problème dans un exercice, pourriez vous m'aider s'il vous plait
On me donne la matrice
)
et je dois montrer que
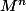
s'écrit sous la forme
)
donc çà j'ai réussi par récurrence
mais ensuite on me demande d'exprimer

et
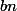
en fonction de n
alors j'ai trouvé que

=

mais pour

je fais des calculs, je m'embrouille un peu, mais je ne trouve rien de récurrent..
auriez vous une idée s'il vous plait? merci
-
hamdo
- Membre Naturel
- Messages: 59
- Enregistré le: 24 Avr 2008, 21:13
-
 par hamdo » 09 Mai 2008, 09:13
par hamdo » 09 Mai 2008, 09:13
Ecrire aussi

en fonction de

et
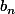
-
neuneu
- Membre Relatif
- Messages: 290
- Enregistré le: 28 Sep 2006, 18:14
-
 par neuneu » 09 Mai 2008, 10:14
par neuneu » 09 Mai 2008, 10:14
Bonjour comme tu sais que bn+1=an , comme dis hamdo exprime an+1 en fonction de an et bn; tu dois avoir trouvé une relation en faisant ta récurrence
tu dois surement te retrouver avec une équation de la forme
an+1 = x*an + y*bn ( toi tu dois avoir des valeurs à la place de x et y mais j'ai pas fait les calculs...)
mais bn=an-1
donc an+1=x*an+y*an-1 ou si tu préfères an+2=x*an+1+y*an
c'est une suite récurrente linéaire d'ordre 2 que je pense que tu sais résoudre
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 09 Mai 2008, 10:24
par Lierre Aeripz » 09 Mai 2008, 10:24
En fait, il n'y a pas besoin de récurrence.
On pose
)
On a alors M = A - 2I.
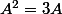
. Donc
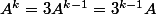
.
Or I et A commutent, donc
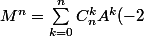^{n-k} I^{n-k})
.
Ce qui donne
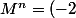^n I + \( \sum_{k=1}^n C_{n}^k 3^{k-1} (-2)^{n-k} \) A)
On calcule
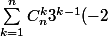^{n-k} = \frac{1}{3} \( (3-2)^n - (-2)^n \))
.
Donc
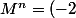^n I + \frac{1 - (-2)^n}{3} A)
.
Bon... J'admets que ce n'est pas tellement plus simple qu'une récurrence.
-
log86
- Membre Relatif
- Messages: 169
- Enregistré le: 25 Nov 2007, 14:17
-
 par log86 » 10 Mai 2008, 12:17
par log86 » 10 Mai 2008, 12:17
Bonjour désolé je n'ai pas pu revenir avant
merci à tous
j'ai compris la méthode de Lierre Aeripz et de neuneu merci
bonne journée
Utilisateurs parcourant ce forum : SAGE63 et 27 invités