Math logique

[typinc]

Beaucoup de misère prouver par le bas (((a imply b) AND (b imply c)) imply (a imply b)).

Merci

[hdci]

Bonjour,

Vous avez écrit



Vous vouliez écrire plutôt ceci n'est-ce pas ?


Pour montrer que c'est toujours vrai (tautologie), vous pouvez faire un tableau de vérité : il contiendra 8 lignes (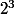 puisqu'il y a 3 propositions : A, B et C) et vous appliquez les règles de vérité de l'implication (toujours vrai sauf hypothèse vraie conclusion fausse).

Vous pouvez également le faire plus synthétiquement ; si A est fausse, la proposition totale est vraie car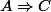 est vraie. De même si C est vraie.
Il n'y a que le cas A vrai et C faux à vérifier : la conclusion étant fausse, il faut s'assurer que l'hypothèse (les deux propositions reliées par ET) est également fausse et il n'y a que deux cas à regarder : B vraie ou B fausse.

[typinc]

Merci d'avoir répondu aussi vite. Par contre je tourne en rond à tenter de prouver C faux.

[hdci]

Si C est fausse et A est vraie, alors 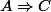est fausse.

Pour que la phrase totale soit vraie, il faut que soit fausse.

Deux valeurs possibles pour B :

• si B est vraie, alors la partie B\Rightarrow C est "vrai implique faux", c'est donc une proposition fausse, et la conjonction est fausse.
• si B est fausse, alors c'est qui est fausse.

Dans les deux cas c'est gagné.