Loi binomiale

[maxou211000]

Bonjour à tous,

J'ai cet exercice que je n'arrive pas à résoudre :
on propose un questionnaire comportant 157 questions. Pour chaque question, il y a 4 réponses possibles. On s'intéresse dans un premier temps à la variable aléatoire X donnant le nombre de réponses correctes à ce questionnaires.

Une réponse correcte rapporte 2 point, et une réponse incorrecte fait perdre 0.5 points. On appelle S le gain obtenu au terme de ce QCM. Le test est réussi si on obtient au moins 40, et la note est ramenée à 0 si le résultat final est négatif.

1) Calculez l'espérance E(X) et sa variance V(X)

2) Exprimer S en fonction de X.



Et donc pour arrondir au dix-millième cela ne va pas.

Merci pour votre aide !

[GaBuZoMeu]

Bonjour,

+1 par bonne réponse, -0.25 par mauvaise, et tu ne sais pas exprimer la note totale en fonction du nombre de bonnes réponses (sachant qu'il y a 100 questions) ?

[maxou211000]

Bonjour,

Pour la question 2, j'ai trouvé S=(5/4)X-25
C'est la question suivante ou je boque : déterminer l'espérance de S , E(S) et sa variance V(S).

[GaBuZoMeu]

Ça ne présente aucune difficulté avec l'expression de S en fonction de X que tu as.
La seule difficulté pourrait être l'ambiguïté sur la définition de S. Il n'est pas clair si "le gain" S désigne bien ce que donne ta formule, ou si S=max((5/4)X-25,0).

[maxou211000]

Je n'ai pas compris

[GaBuZoMeu]

Dommage. Qu'est-ce que tu n'as pas compris ?

[maxou211000]

ma formule : S=(5/4)X-25
Si on remplace X par le nb de bonne réponse, cela nous donne la note.
Mais je n'arrive pas à exprimer déterminer l'espérance de S , E(S) et sa varience
Je sais que l'espérence c'est : n*p

[GaBuZoMeu]

Hum.
Soit une variable aléatoire réelle, et soient et des constantes réelles. Tu ne sais pas exprimer l'espérance et la variance de en fonction de l'espérance et la variance de ?

Par ailleurs, il est précisé dans l'énoncé qu'une note négative est ramenée à 0. Donc la formule pour la note est en fait . Ça complique les choses !

[maxou211000]

Non je ne sais pas

[tournesol]

pour la question 3 , j'ai (casio graph 35+) 4,3240189x10^(-8)
Ton prof à du vouloir dire :arrondir à 4 décimales la mantisse de l'écriture scientifique de ta réponse donc à 4,3240x10^(-8)

[GaBuZoMeu]

Non je ne sais pas

Relis bien ton cours pour voir s'il n'y a vraiment aucune information sur l'espérance et la variance de en fonction de l'espérance et de la variance de .
Et si tu ne vois rien, reviens aux définitions d'espérance et de variance !

[maxou211000]

Ok merci bcp GaBuZoMeu j'ai trouver !
il ne me reste plus qu'à trouver la probabilité d'avoir la moyenne

[GaBuZoMeu]

Qu'as-tu trouvé, si ce n'est pas indiscret ?

[maxou211000]

Il faut 60 bonnes réponses pour avoir la moyenne
Donc à la calculatrice : 1-BinomialCD(59,100,1/3)
Ce qui fais 4.32*10^-8
Impossible donc d'arrondir au dix milième

[GaBuZoMeu]

Le résultat est correct, et il est tout à fait possible de l'arrondir au dix-millième : quelle est la partie entière de ce résultat multiplié par 10 000 ?

[ManelB]

Bonjour, J’ai un exercice qui ressemble à celui-ci, mais je ne comprends pas totalement vos réponses finales car X ≥ 20 vu que S n’est pas négatif.
Du coup j’ai fait cela qu’en pensez vous s’il vous plait, merci par avance.

La note finale S ne peut pas être négative donc X est forcément supérieur ou égal à 20 : X ≥ 20
Donc P(X ≥ 60) = 1 - P(20 ≤ X ≤ 59)
<=> P(X ≥ 60) = 1 - P(20 ≤ X ≤ 59)
or P(20 ≤ X ≤ 59) = P(X ≤ 59) - P(X ≤ 19)) car les événements sont indépendants
Pour cela on calcule avec la calculatrice Casio 35+ P(20 ≤ X ≤ 59) :
BinomialCD(59,100,1/3) et BinomialCD(19,100,1/3)
De là on obtient le résultat tel que :
P(X ≥ 60) = 1 - P(20 ≤ X ≤ 59)
car si je calcule P(20 ≤ X ≤ 59) = P(X ≤ 59) - P(X ≤ 20)
Après je trouve : P(X ≥ 60) = 1 - P(20 ≤ X ≤ 59) ≈ 0,0024 qui est un résultat au dix millième près

Merci.

[GaBuZoMeu]

Bonjour,

Déjà, Maxou a changé l'énoncé après avoir reçu les réponses. Pourquoi a-t-il fait ça ?

Ensuite ton interprétation n'est pas bonne : on peut très bien avoir X<20, mais alors la note qui devait être négative d'après le barème est ramenée à 0.
Donc la suite de tes calculs n'a pas de sens.

[ManelB]

Merci beaucoup pour votre réponse.
Je ne sais pas pourquoi il a changé l énoncé ?

Si on peut avoir X<20, alors comme S = 5/4X-25 donc S peut être <0 et dans ce cas la note S sera ramenée à 0, en effet.
Ainsi qu en est il de la probabilite de X<20 sachant que P(S<0) = 0. Peut on dire que P(X<20) = 0 ?
Merci

[GaBuZoMeu]

Bien sûr que non.

Je rappelle ce que j'ai déjà écrit : .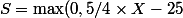
L'événement n'est certainement pas de probabilité nulle.
Je ne retrouve pas dans l'énoncé la probabilité de donner une bonne réponse. Ça a peut-être été supprimé par maxou.

[ManelB]

La probabilité de donner une bonne réponse était p=1/3 car X suit une binomiale (100,1/3).
Vous me dites non à mes questions mais vous ne m expliquez pas pourquoi.
Je suis d accord vous, mais je voudrais vraiment comprendre. Merci