Logiciel mathématique
15 messages
- Page 1 sur 1
logiciel mathématique
Bonsoir
j'ai un système d'équations
X=a+b*exp(-y/c)
avec x=[52,33,19,11,7]
y=[0,10,25,50,85]
on cherche à déterminer a,b et c
est ce que c'est possible de résoudre ce problème à l'aide d'un logiciel mathématique (Matlab, scilab, maple)
est ce que c'est possible de déterminer cette équation à partir de la courbe,
Merci pour votre aide
j'ai un système d'équations
X=a+b*exp(-y/c)
avec x=[52,33,19,11,7]
y=[0,10,25,50,85]
on cherche à déterminer a,b et c
est ce que c'est possible de résoudre ce problème à l'aide d'un logiciel mathématique (Matlab, scilab, maple)
est ce que c'est possible de déterminer cette équation à partir de la courbe,
Merci pour votre aide
salut
ce genre d'estimation de paramètres s'appelle de la régression
en général on peut pas trouver a,b et c qui satisfassent X=f(y) pour tout x et tout y dans tes données (tu as 3 paramètres qui doivent satisfaire 5 équations => redondance/incompatibilité).
En général, on se contente de a, b et c tels que la somme des |x-f(y)|^2 soit minimale. On considère cette somme comme une fonction de a,b et c g(a,b,c). (on cherche a minimiser la somme des erreurs au carré commises en approximant x par f(y))
Alors il suffit de trouver le minimum de g sur R^3. C'est assez facile quand f est polynomiale par exemple. Parcontre dans le cas général ca peut etre assez compliqué, on essaye de se ramener (par un changement de variable sur y) au cas où f est polynomiale mais ca n'est pas tjs possible
ce genre d'estimation de paramètres s'appelle de la régression
en général on peut pas trouver a,b et c qui satisfassent X=f(y) pour tout x et tout y dans tes données (tu as 3 paramètres qui doivent satisfaire 5 équations => redondance/incompatibilité).
En général, on se contente de a, b et c tels que la somme des |x-f(y)|^2 soit minimale. On considère cette somme comme une fonction de a,b et c g(a,b,c). (on cherche a minimiser la somme des erreurs au carré commises en approximant x par f(y))
Alors il suffit de trouver le minimum de g sur R^3. C'est assez facile quand f est polynomiale par exemple. Parcontre dans le cas général ca peut etre assez compliqué, on essaye de se ramener (par un changement de variable sur y) au cas où f est polynomiale mais ca n'est pas tjs possible
niniiii a écrit:est ce que c'est possible de résoudre ce problème à l'aide d'un logiciel mathématique (Matlab, scilab, maple)
salut,
c'est moi le logiciel mathémathic.Comme le repas de midi a été bien arrosé,je ne sais si je tiendrai jusqu'au bout des calculs :dingue2:
Comme l'a bien indiqué Kazériahm, il suffit de trouver le minimum
de la fonction de trois variables:
on a posé les fonctions réelles croissantes,positives:
on calcule les coordonnées de df(a,b,c) dans la base duale pour les annuler,
puisque nous cherchons un minimum
on pose , par commodité,
où l'on commence à différentier à tout va
re,
la dérivée de f par rapport à a:
 \right) (-1)=0)
soit:

la dérivée de f par rapport à b:
 \right) (-u_i) = 0)
soit:
= E(xu))
la dérivée de f par rapport à c:
 \right) (-b \frac{y_i u_i}{c^2}) = 0)
soit:
 +b E(yu^2)= E(xyu))
 u est une fonction du paramètre
u est une fonction du paramètre 
la dérivée de f par rapport à a:
soit:
la dérivée de f par rapport à b:
soit:
la dérivée de f par rapport à c:
soit:
re,
les deux premières égalités (système Cramer 2x2) donnent
-\bar{u} E(xu)}{Var(u)})
 - \bar{u} \bar{x}}{Var(u)})
on remplace dans la troisième égalité:
 \left( \bar{x} E(u^2) - \bar{u} E(xu) \right) +E(yu^2) \left( E(xu)- \bar{u} \bar{x} \right) - E(xyu) Var(u) = 0)
(***)
en ayant posé:
 = \frac{1}{n} \sum_{i} y_i u_i(c))
 =\frac{1}{n} \sum_{i} x_i y_i u_i(c))
 = \frac{1}{n} \sum_{i} x_i)
 = \frac{1}{n} \sum_{i} u_i^2(c))
)
etc..
l'égalité (***) ( les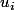 étant des fonctions
étant des fonctions
de la variable c) donne c , comme solution d'une équation implicite.
il y a juste besoin de demander à la calculette (TI89 ?) les solutions.
je t'ai donc ramené un problème facile à trois variables à
un problème (compliqué) à une variable :zen:
ceçi dit, ça doit pas être si compliqué car
où l'on pose
qui va rentrer la formule dans la calculette, elle doit faire dans les 800
caractères ? :hum: . Faut la développer formellement...
les deux premières égalités (système Cramer 2x2) donnent
on remplace dans la troisième égalité:
(***)
en ayant posé:
etc..
l'égalité (***) ( les
de la variable c) donne c , comme solution d'une équation implicite.
il y a juste besoin de demander à la calculette (TI89 ?) les solutions.
je t'ai donc ramené un problème facile à trois variables à
un problème (compliqué) à une variable :zen:
ceçi dit, ça doit pas être si compliqué car
où l'on pose
qui va rentrer la formule dans la calculette, elle doit faire dans les 800
caractères ? :hum: . Faut la développer formellement...
busard_des_roseaux a écrit:re,
(***)
en ayant posé:
etc..
là, je suis ennuyé. Cette somme est une combinaison linéaire toute bête
d'exponentielles de la forme
Cette somme (nulle) donne une équation, dont le coeff
équation S(c)=0. Le souçi, la somme S est une combinaison linéaire de 450 exponentielles. On calcule la fonction dérivée de S, chiche ?
Bonjour.
Voici un exemple :
[img][IMG]http://img25.imageshack.us/img25/3504/regrexpjpg.jpg[/img][/IMG]
Voici un exemple :
[img][IMG]http://img25.imageshack.us/img25/3504/regrexpjpg.jpg[/img][/IMG]
où je reprend à zéro !!
re,
la différentielle nulle donne le système à 2 inconnues (a,b),
le coefficient c est "caché" comme variable de la pseudo-"fonction" u:
= E(xu) \\<br />\displaystyle a E(yu) +b E(yu^2)= E(xyu))
Ce système n'est pas un système de Cramer. On écrit qu'il admet
bien une solution en annulant le déterminant suivant:
 & \quad E(xu) \\<br />\displaystyle E(yu) & \quad E(yu^2) & \quad E(xyu) <br />\end{array}=0)
soit ;
-\bar{u}^2 & \quad E(xu)-\bar{x}\bar{u} \\<br />\displaystyle E(yu) & \quad E(yu^2)-\bar{u}E(yu) & \quad E(xyu)-\bar{x}E(yu) <br />\end{array}=0)
en développant par rappport à la 1ère ligne:
-\bar{u}^2 & \quad E(xu)-\bar{x}\bar{u} \\<br />\displaystyle E(yu^2)-\bar{u}E(yu) & \quad E(xyu)-\bar{x}E(yu) <br />\end{array} = 0)
par distributivité
-\bar{u}^2 & \quad E((x-\bar{x})u) \\<br />\displaystyle E(yu^2)-\bar{u}E(yu) & \quad E((x-\bar{x})yu) <br />\end{array} = 0)
où
-\bar{u}^2=\frac{4}{25} \left( 1+e^{ - \frac{20}{c}}+e^{ - \frac{100}{c}}+e^{ - \frac{170}{c}} \right) -\frac{2}{25} \left( e^{ - \frac{10}{c}}+e^{ - \frac{25}{c}}+e^{ - \frac{35}{c}}-e^{ - \frac{50}{c}} +e^{ - \frac{60}{c}}+e^{ - \frac{75}{c}}+e^{ - \frac{80}{c}}+e^{ - \frac{95}{c}}+e^{ - \frac{110}{c}}+e^{ - \frac{135}{c}}\right))
on voit que si les (y_i) sont en progression arithmétique, ça divise le nombre de termes des sommes par n (la taille de l'échantillon).
Que d'autre part, on notera formellement une somme de k exponentielles
par un k-uplet d'exposants.
Comme on multiplie des combinaisons linéaires de morphismes, quelle structure ? algèbre ? produit semi-direct ?
la différentielle nulle donne le système à 2 inconnues (a,b),
le coefficient c est "caché" comme variable de la pseudo-"fonction" u:
Ce système n'est pas un système de Cramer. On écrit qu'il admet
bien une solution en annulant le déterminant suivant:
soit ;
en développant par rappport à la 1ère ligne:
par distributivité
où
on voit que si les (y_i) sont en progression arithmétique, ça divise le nombre de termes des sommes par n (la taille de l'échantillon).
Que d'autre part, on notera formellement une somme de k exponentielles
par un k-uplet d'exposants.
Comme on multiplie des combinaisons linéaires de morphismes, quelle structure ? algèbre ? produit semi-direct ?
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
