Bonjour à tous,
J'aimerais calculer 2 limites :
L'application f est telle que f(x)=(ln(x))^(n) * x^(1/2) (racine de x) avec n un entier naturel non nul
Je cherche la limite en 0+ de f et en +infini de x--> f(x)/x
J'ai tout essayé : changement de variable, factorisation, croissance comparée avec le théorème des gendarmes et rien n'aboutit.
Merci de votre aide !
Limites composés (ln(x))^n * x^(0,5)
14 messages
- Page 1 sur 1
Je suis d'accord mais le problème c'est que c'est valable pour le même a et b sinon comment démontrer cette croissance comparée ?
De plus ce n'est pas sur x^b mais (racine(x))^b mais cela tend aussi vers 0 en utilisant le htm des gendarmes.
Donc comment démontrer la croissance comparée (que un terme tend plus vite que l'autre), avec a différent de b (a et b les exposants)?
De plus ce n'est pas sur x^b mais (racine(x))^b mais cela tend aussi vers 0 en utilisant le htm des gendarmes.
Donc comment démontrer la croissance comparée (que un terme tend plus vite que l'autre), avec a différent de b (a et b les exposants)?
Si tu ne connais pas
 et
et 
^{\beta}=o(x^{\alpha})) au voisinage de
au voisinage de  ?
?
regarde dans un livre de maths ou sur internet la démonstration de cette propriété (si elle t'intéresse)
C'est est une propriété très connue et souvent utilisée
Et qui permet de répondre à la question de ton exo : Quelle est la limite de f(x)/x quand x tend vers +infini
ps)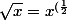})
regarde dans un livre de maths ou sur internet la démonstration de cette propriété (si elle t'intéresse)
C'est est une propriété très connue et souvent utilisée
Et qui permet de répondre à la question de ton exo : Quelle est la limite de f(x)/x quand x tend vers +infini
ps)
pour démontrer queitaipe a écrit:D'accord mais je ne trouve pas la démonstration sur internet et pour la limite en 0+ tu aurais une idée ?
il suffit de démontrer que
Est ce que tu sais faire cette démonstration (dont le résultat est très souvent utilisé, déjà au lycée en TS ou TES)
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
