Limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 25 Aoû 2007, 17:32
par Sylar » 25 Aoû 2007, 17:32
Bonjour,
je bloque sur cet exo:
Trouver pour a appartenant a ]0,+inf[ fixé ,
lim(n-> +inf) Sum[k=1...n] [ 1-a.(k/n) ]^n
merci ....
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 25 Aoû 2007, 18:16
par B_J » 25 Aoû 2007, 18:16
Salut ;
dx}))
?
a verifier ...
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 25 Aoû 2007, 19:24
par Sylar » 25 Aoû 2007, 19:24
J'en ai aucune idée mais je vois pas d'ou tu sors ca ....
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 25 Aoû 2007, 20:00
par Edrukel » 25 Aoû 2007, 20:00
numériquement c'est faux , j'ai pris a=2 avec Maple :-)
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 25 Aoû 2007, 20:21
par Edrukel » 25 Aoû 2007, 20:21
Sylar
Est-ce que c'est bien ce que tu voulais nous écrire ::
^n})
?
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 25 Aoû 2007, 20:38
par Sylar » 25 Aoû 2007, 20:38
Oui c'est ça ....
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 25 Aoû 2007, 20:58
par Edrukel » 25 Aoû 2007, 20:58
c'est quoi la source ?
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 26 Aoû 2007, 13:25
par B_J » 26 Aoû 2007, 13:25
Bonjour;
soit
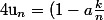^n)
et
) theoreme
theoreme:

, continue par morceaux sur

; on a :
dx=\lim_{n\to+\infty} \frac{\beta-\alpha}{n} \sum_{k=0}^{n-1}f(\alpha+k\frac{\beta-\alpha}{n}))
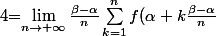)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Aoû 2007, 13:51
par Nightmare » 26 Aoû 2007, 13:51
Plus qu'un théorème c'est presque la définition même de l'intégrale de Riemann...
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 27 Aoû 2007, 11:17
par Edrukel » 27 Aoû 2007, 11:17
je ne crois pas que la solution soit ça :*)
essayer de montrer que ça tend vers sum(exp(-ka),k=1..+oo) pour a
note :: il y'a convergene pour a<=2
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 27 Aoû 2007, 13:14
par quinto » 27 Aoû 2007, 13:14
Nightmare a écrit:Plus qu'un théorème c'est presque la définition même de l'intégrale de Riemann...
Non pas du tout.
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 27 Aoû 2007, 13:21
par Sylar » 27 Aoû 2007, 13:21
On peux pas utiliser les intégrales de Riemman ici !
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 27 Aoû 2007, 14:23
par Edrukel » 27 Aoû 2007, 14:23
pour 02 , divergence

-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 27 Aoû 2007, 14:57
par Sylar » 27 Aoû 2007, 14:57
En utilisant le théorème de convergence dominé je trouve:
L= exp(-a) /[1-exp(-a)] = 1/[ exp(a) -1]
-
matthieu l.
- Messages: 1
- Enregistré le: 27 Juin 2007, 16:22
-
 par matthieu l. » 27 Aoû 2007, 15:43
par matthieu l. » 27 Aoû 2007, 15:43
Sylar a écrit:Bonjour,
je bloque sur cet exo:
Trouver pour a appartenant a ]0,+inf[ fixé ,
lim(n-> +inf) Sum[k=1...n] [ 1-a.(k/n) ]^n
merci ....
Salut,
ça donne quelque chose si tu réduis le terme de la série en utilisant la formule du binôme de newton ?
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 27 Aoû 2007, 16:05
par Edrukel » 27 Aoû 2007, 16:05
Sylar, tu as utilisé ce que j'ai donné pour obtenir L ?
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 27 Aoû 2007, 16:16
par Sylar » 27 Aoû 2007, 16:16
Non j'ai utilisé le théorème de convergence dominé ....
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 27 Aoû 2007, 16:28
par Edrukel » 27 Aoû 2007, 16:28
comment tu as fait,expliques stp :-)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
