limite à 0
Limite
8 messages
- Page 1 sur 1
Re: Limite
par Carpate » 07 Sep 2016, 03:02
c quelqu'un peut calculer
Qui pourrait m'expliquer la syntaxe de ce "c quelqu'un peut calculer" ?
Re: Limite
par Kolis » 07 Sep 2016, 07:55
Je ne peux pas expliquer la syntaxe mais je "peux" calculer la limite...
Re: Limite
par Razes » 07 Sep 2016, 08:03
Développement limité au voisinage de zéro.
=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots +(-1)^{n}{\frac {x^{{2n+1}}}{(2n+1)!}}+o(x^{2n+2})\\\\\cos(x)=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots +(-1)^{n}{\frac {x^{{2n}}}{(2n)!}}+o(x^{{2n+1}}))
ou deux fois la règle de L'Hôpital
Résultat
ou deux fois la règle de L'Hôpital
Résultat
Re: Limite
par Kolis » 07 Sep 2016, 11:47
Ou aussi : =\sin(\frac{\pi}2-\frac{\pi}2\cos x)=\sin(\frac{\pi}2(1-\cos x)))
.
Comme
on a aussi \underset{x\to0}\simeq\frac{\pi x^2}4)
.
Par ailleurs,\underset{x\to0}\simeq\sin x)
donc le dénominateur est équivalent à 
.
Finalement, sauf erreur, la limite est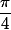
@Razès : le développement limité de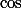
en 0 ne suffit pas puisqu'il apparaîtra +\dots))
et il faudrait un développement limité de 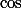au voisinage de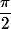 
Comme
Par ailleurs,
Finalement, sauf erreur, la limite est
@Razès : le développement limité de
Re: Limite
par aymanemaysae » 07 Sep 2016, 13:21
Bonjour;
On a :
) = x^2 \dfrac{\sin(x)}{x} \dfrac{\sin(\sin(x))}{\sin(x)})
et) = \sin(\frac{\pi}{2}(1-\cos(x))= \frac{\pi}{2} (1-\cos(x)) \dfrac{\sin(\frac{\pi}{2}(1-\cos(x)))}{\frac{\pi}{2}(1-\cos(x))})
donc)}{x\sin(\sin(x))} = \frac{\pi}{4} \dfrac{1-\cos(x))}{\frac{x^2}{2}} \dfrac{\dfrac{\sin(\frac{\pi}{2}(1-\cos(x)))}{\frac{\pi}{2}(1-\cos(x))}}{\dfrac{\sin(x)}{x}\dfrac{\sin(\sin(x))}{\sin(x)}})
et comme on a}{x} = \lim_{x\rightarrow 0} \dfrac{1-\cos(x))}{\frac{x^2}{2}} = 1)
donc)}{x\sin(\sin(x))} = \dfrac{\pi}{4})
Edit : j'ai posté cette solution dans le but de m'enquérir des nouvelles de M.Robot, j'espère qu'il va bien : ça fait longtemps qu'il ne s'est pas manifesté sur ce "Forum" .
On a :
et
donc
et comme on a
donc
Edit : j'ai posté cette solution dans le but de m'enquérir des nouvelles de M.Robot, j'espère qu'il va bien : ça fait longtemps qu'il ne s'est pas manifesté sur ce "Forum" .
Re: Limite
par Razes » 07 Sep 2016, 15:05
Kolis a écrit:@Razès : le développement limité de
T’inquiétè pas, je n'allais pas procéder à un développement limité de
@aymanemaysae
J'aime bien tes
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :