Limite de n!/n^n.

[ezril13]

Bonjour,

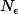
Montrer que en appliquant la définition de la convergence et en précisant qui intervient dans cette définition.

On arrive à montrer que la limite est 0 avec le théorème des gendarmes en montrant que c'est infèrieur à .

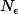
On doit ensuite trouver tel que :


Je ne vois pas comment résoudre cette dernière inégalité.

Je précise que l'exercice est au niveau L1 math.

Merci.

[Doraki]

ben si tu sais que n!/n^n <= 1/n, il te suffit de trouver N;) tel que pour tout n, n > N;) => 1/n < ;)

[ezril13]

Ca résout le problème quand .

Mais lorsque ?

[Doraki]

On te demande de trouver pour chaque ;), un N;) qui vérifie une certaine propriété
N;) dépend de ;) et de rien d'autre.
"n" n'existe pas quand on se demande si pour tout ;) il existe bien N;) tel que (...) Donc se demander ce qui se passe quand ;) < 1/n n'a absolument aucun sens.

Moi j'ai dit que si tu arrives à trouver pour chaque ;), un N;) qui vérifie (pour tout n, (n > N;)) => (1/n < ;)))
alors tu as fini parce qu'alors pour chaque ;) tu as trouvé un N;) qui vérifie (pour tout n, (n > N;)) => (n!/n^n < ;))) : en effet, pour un tel n, n!/n^n < 1/n et 1/n < ;) donc n!/n^n < ;).