Limite fonction trigonométriques.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 28 Oct 2021, 21:23
par novicemaths » 28 Oct 2021, 21:23
Bonsoir
Dans mon livre d'analyse niveau L1, je ne vois rien sur les règles de calculs avec les fonctions trigonométriques avec pi.
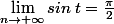
Pour la limite ci-dessous, je ne vois pas comment raisonner. J'ai considéré l'infinie comme zéro, car si j'ai bien compris on ne peut pas déterminer de limite en infinie avec les fonctions trigonométriques.
 = \frac{ \pi}{2})
Pourriez-vous me corriger et m'expliquer clairement les règles à suivre pour l'étude de limite avec les fonctions de trigonométriques.
Merci !!
A bientôt
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 28 Oct 2021, 22:08
par tournesol » 28 Oct 2021, 22:08
Bonsoir
ta première limite est égale à sin t .
ta deuxième limite est égale à 1 .
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 28 Oct 2021, 22:18
par novicemaths » 28 Oct 2021, 22:18
Merci tournesol.
Je souhaiterais comprendre, pars ce que je suis un peu perdue.
Avec les fonctions trigonométriques, si j'ai bien compris l'infinie ne vaut rien.
A bientôt
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 29 Oct 2021, 07:46
par tournesol » 29 Oct 2021, 07:46
les deux suites que tu proposes sont des suites constantes .
La première parceque n n'y figure pas .
La deuxieme parceque sin est 2pi périodique .
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 31 Oct 2021, 17:10
par novicemaths » 31 Oct 2021, 17:10
Bonjour
Voici deux nouvelles études de limites.
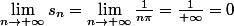
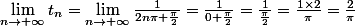
J'ai détaillé le plus possible mon raisonnement afin de comprendre mes erreurs de raisonnement.
Je vous l'avoue, je suis un peu perdu avec les limites de suite avec pi.
A bientôt

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 31 Oct 2021, 18:00
par Ben314 » 31 Oct 2021, 18:00
Salut,
novicemaths a écrit: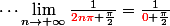
Tu es vraiment sûr que, quand on fait 100 x 3,14, puis 1 000 x 3,14 puis 10 000 x 3,14, ça donne comme résultat des nombres de plus en plus proche de zéro ?
Bref, un minimum de bon sens, ça ne nuit jamais . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 31 Oct 2021, 19:02
par novicemaths » 31 Oct 2021, 19:02
C'est une simple étude de limite, pi me fait paniquer un peu.
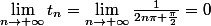
Est-ce que là c'est correct ?
A bientôt
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
