Les intégrales à paramètre

[aissayoub]

Bonsoir , quelqu'un a une idée pour la question 1.3, j'arrive pas à majorer la dérivée partielle par une fonction intégrable ?

[GaBuZoMeu]

As-tu utilisé l'indication donnée dans l'énoncé ?
On dirait que ça entraîne du côté de l'intégration par parties.

[aviateur]

Bonjour
Il faut comprendre que le théorème de dérivation ne s'applique ici puisque la seconde intégrale n'est pas absolument convergente. Ceci pour dire qu'on ne majore pas uniformément la fonction qui est sous le signe somme par une fonction intégrable.
Mais alors l'idée simple serait de réécrire l'intégrale qui donne autrement, de telle sorte qu'on puisse appliquer ce théorème.
Pour cela le terme 1/(1+t^2), si on le dérive on va augmenter la décroissance vers 0 par un facteur de 1/t^2 et avec l'intégration de exp(i tx) on aura un facteur au total de 1/t.
Autrement dit faire une IPP sur va permettre d'appliquer le théorème de dérivation.
Ainsi on aura la réponse à la question sauf que l'intégrale qui donne n'est pas sous la forme donnée.
Il restera à simplifier pour arriver au résultat.

[GaBuZoMeu]

Pour cela le terme 1/(1+t^2), si on le dérive on va augmenter la décroissance vers 0 par un facteur de 1/t^2 et avec l'intégration de exp(i tx) on aura un facteur au total de 1/t.

Hum hum ... Double erreur qui se compense. Quand on dérive , (qui est équivalent à au voisinage de ), on a quelque chose d'équivalent à ; pas de facteur !
Et quand on intègre (par rapport à ), on a un facteur qui apparaît, pas de à l'horizon !

[aviateur]

Bon, Je crois qu'il est assez grand pour corriger. L'idée est là c'est l'essentiel.

[GaBuZoMeu]

Elle était dans l'indication de l'énoncé.

[aviateur]

Non pas du tout. L'indication c'est "on pourra dériver t/(1+t^2)."
J'appelle pas ça une indication. Ou alors c'est une erreur de l'auteur. C'est pas pareil si il avait dit on pourra dériver 1/(1+t^2).
Alors oui, ça laisserait penser faire une ipp
Et je suis d'accord que quand tu dis ça fait penser à faire une ipp, ça peut aider ; mais ajouté à l'indication donnée ça laisse encore perplexe.
C'est pour ça que je précise de faire une ipp sur .
Donc si tu fais une ipp sur phi comme ça de tête ça améliore surement les choses, j'ai ren écrit mais je sais qu'on a du 1/t^3 et que ça doit (devrait marcher). Effectivement n'ayant rien écrit je fais une erreur dans l'explication de ce sur quoi on doit arriver mais maintenant c'est à lui de prendre les manettes.

[GaBuZoMeu]

Il est convenable de faire l'IPP non pas sur l'intégrale donnant , mais sur celle donnant 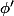pour montrer qu'on a bien convergence, uniforme en sur tout compact. C'est ce que suggère l'énoncé, en demandant de dériver . C'est une bonne indication et ce n'est pas l'auteur de l'exercice qui se fourvoie dans cette affaire.

[aviateur]

Mais bon, mets toi à ma place ou bien à la place de n'importe quel quidam qui comprend un peu les mathématiques.
Si sans indication je vois comment il faut faire, est-ce que l'exercice consiste à deviner ce que l'auteur à voulu faire (c'est à dire à suivre son indication) ou alors à résoudre par soi même faire l'exercice?
C'est à dire en suivant son propre chemin, qui sera le même ou plus ou moins bien.

Maintenant quel ton but?

[GaBuZoMeu]

Maintenant quel ton but?

D'aider le questionneur ou la questionneuse, en l'incitant entre autres à tirer parti des indications données dans l'énoncé.

Et toi quel est ton but ? Pourquoi affirmer que "J'appelle pas ça une indication. Ou alors c'est une erreur de l'auteur", alors que l'indication donnée va bien dans le sens qui me semble le plus naturel : c'est de la convergence de l'intégrale exprimant la dérivée qu'on doit se préoccuper pour assurer le caractère de !

[aviateur]

Ah, bon! Comme si ce que je propose ne s'occupe pas du caractère de et de la possibilités d'appliquer le th de dérivation des intégrales paramétrées.

Mais quel perte de temps inutile encore une fois.

[GaBuZoMeu]

Mais quel perte de temps inutile encore une fois.

À qui la faute ? Pourquoi ne pas avoir laissé le questionneur ou la questionneuse travailler avec l'indication parfaitement valable de l'énoncé et se croire obligé de donner une autre indication, farcie d'erreurs ?

[aviateur]

Bon là tu pousses encore loin le bouchon. Tu sais très bien que si dans un raisonnement, si je mets 1/2+1/3=1, les personnes intelligentes comprendront de quelle sorte d'erreur il s'agit.
Maintenant, au niveau des erreurs, tu veux que je mette le lien où tu as une fonctionnelle de matrices et où tu n'a pas su calculer correctement la fonctionnelle?
J'ai noté avec respect ton erreur, mais il y a des chances celui qui a posé la question n'a pas compris.

[GaBuZoMeu]

tu veux que je mette le lien où tu as une fonctionnelle de matrices et où tu n'a pas su calculer correctement la fonctionnelle?

Tu fais allusion à ce fil, je suppose : dérivation d'une formule matricielle
Au fait, tu n'es pas intervenu pour dire si l'erreur que tu avais vue était bien celle que j'avais trouvée et corrigée. C'était bien celle-là ?

Je constate que tu te plains d'une perte de temps, mais que tu t'embarques dans une histoire qui n'a rien à voir avec ce fil. Puisqu'on en est à la perte de temps, une question qui m'intrigue : le "92" indiqué dans ton profil, c'est ton âge ou ton année de naissance ?

[aviateur]

Bon j'avais pas fini mon message.

Je vais perdre mon temps une dernière fois avec toi.

1. Tu dis que l'indication de l'énoncé suffit en elle même. Donc le posteur n'a qu'à se débrouiller avec? A quoi ça sert de l'aider.

2. Je lui dit de faire une IPP sur l'intégrale (on sera amené à dériver 1/(1+t^2) et c'est pour ça que j'ai pense qu'il y a une erreur dans l'indication).
Avec cette IPP on va se ramener à une nouvelle expression de l'intégrale où on pourra appliquer le théorème de dérivabilité sans problème. On pourra aussi avoir la continuité de

Comment oses tu dire que ce je proposes est truffé d'erreur (uniquement parce que la dérivée que je donne n'est pas bonne alors que c'est simplement rectifiable) ?

J'espère que celui qui a posé la question comprend que c'est la bonne voie.

3. Pour terminer l'intégrale obtenue pour demandera une petit travail pour arriver à

Maintenant concernant l'indication de l'énoncé, si tu estimes qu'elle bonne, pourquoi pas?

Mais alors tu expliqueras à @aissayoub comment il va intégrer par parties l'intégrale de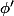 qui est donnée dans l'énoncé alors qu'a priori, on ne sait pas si elle est convergente.
Parce c'est pas donné de suivre cette voie, du moins c'est ce que je pense.
Et c'est pourquoi que ce je propose est surement plus simple jusqu'à preuve du contraire.
Alors mouille-toi un peu et explique comment il va faire .

C'est pas en clamant de façon régulière que ce que je dis est bidon, en te servant de mes petites erreurs (qui sont de l'ordre de l'erreur de frappe et que je fais cela de tête), que c'est bidon .


En soi même j'en ai rien à faire. Mais je perds mon temps car tout de même, c'est des math que je dois défendre et ça me prends du temps uniquement parce tu t'amuses à affirmer ce qui est vrai est faux.

[GaBuZoMeu]

Alors tu expliqueras au poseur de la question comment il va intégrer par parties l'intégrale de qui est donnée dans l'énoncé alors qui a priori, on ne sait pas qu'elle est convergente.

Cette incompréhension de ta part me surprend. Justement, l'intégration par parties (avec dérivation de comme dit dans l'indication) permet de démontrer la convergence de l'intégrale, convergence uniforme en sur tout compact. La limite est donc bien continue en et c'est la dérivée par rapport à de . Je n'en dis pas plus pour ne pas tout divulgâcher, mais j'espère que ça te suffit pour enfin comprendre.

Tu ne veux pas répondre sur le 92 ?

[fatal_error]

Bonjour messieurs,

cela fait plusieurs fois déjà.
Je ne suis pas sûr que vos proses intéressent grand monde, et même si c'est le cas, ce qu'il en ressort, c'est quelquechose de confus_ant_ et pas très convivial non plus.

Je vous invite à continuer cet échange par mp.

Je vous propose également de vous abstenir de poster l'un sur les interventions de l'autre, ou peut être seulement une fois que l'exercice a été résolu par l'auteur.

Il est bien sûr toléré d'intervenir sur une discussion où il y a déjà un aidant, mais il est généralement élégant de laisser le canal "privilégié" déjà établi, sauf si on voit que la discussion s'embourbe (ce qui n'est pas le cas ici, l'auteur étant probablement encore dans son lit à 7h23)

[aissayoub]

Merci beaucoup à tous vous m'avez vraiment aidé !

[aissayoub]

As-tu utilisé l'indication donnée dans l'énoncé ?
On dirait que ça entraîne du côté de l'intégration par parties.

Merci pour votre aide pour le meme exercice est ce que vous avez une idée sur la question 1.6

[aissayoub]

Bonjour
Il faut comprendre que le théorème de dérivation ne s'applique ici puisque la seconde intégrale n'est pas absolument convergente. Ceci pour dire qu'on ne majore pas uniformément la fonction qui est sous le signe somme par une fonction intégrable.
Mais alors l'idée simple serait de réécrire l'intégrale qui donne autrement, de telle sorte qu'on puisse appliquer ce théorème.
Pour cela le terme 1/(1+t^2), si on le dérive on va augmenter la décroissance vers 0 par un facteur de 1/t^2 et avec l'intégration de exp(i tx) on aura un facteur au total de 1/t.
Autrement dit faire une IPP sur va permettre d'appliquer le théorème de dérivation.
Ainsi on aura la réponse à la question sauf que l'intégrale qui donne n'est pas sous la forme donnée.
Il restera à simplifier pour arriver au résultat.

Merci pour votre aide pour le meme exercice est ce que vous avez une idée sur la question 1.6