Les intégrales à paramètre

[GaBuZoMeu]

Si on te donne l'indication de subdiviser l'intervalle , c'est sans doute pour que tu t'intéresses à

où est un réel bien choisi (et indépendant de ).
La question 1.5 demande de t'intéresser à la différence . Sans doute pour te pousser à décomposer


Peux-tu trouver des choses intéressantes à dire (relativement au comportement quand ) pour chacun des deux morceaux ? Il restera bien sûr aussi à étudier le reste




PS. Ça serait sympa de donner un petit retour sur les indications qu'on peut te donner : pas seulement "Merci", ce qui est gentil, mais aussi ce que tu as pu finalement faire.

[aissayoub]

Merci de votre réponse , j'ai trouvé à partir de votre indication que et je vois pas ce qui est intéressant dans cette majoration

[GaBuZoMeu]

En procédant comme je l'indique et sans grande imagination, je trouve un équivalent à pour . Ça me semble aller dans la bonne direction.
Retourne à tes calculs, tu trouveras aussi cet équivalent.

[aissayoub]

je vois pas comment vous avez fait pour appliquer la question 1.5 sans faire apparaitre le module .

[aviateur]

Est ce que tu as vu mon MP?

[aissayoub]

oui je viens de le voir , je vous ai répondu .

[GaBuZoMeu]

Pourquoi faire des cachotteries, aviateur ? Si tu as des choses à dire sur ce fil, dis-les dans ce fil pour que tout le monde puisse en profiter!

Pour aissayoub : je t'ai indiqué


As-tu calculé le premier morceau ? C'est bien sûr lui le plus intéressant dans la recherche d'un équivalent.
La question 1.5 sert pour majorer en module le deuxième morceau.

[aviateur]

C'est bien @Gabuzomeu, tu es peut-être sur la bonne voie.
Concernant le MP, c'est privé, mais bon j'ai demandé à @aissayoub si il allait bien. Il m'a dit que oui.

[aissayoub]

Pourquoi faire des cachotteries, aviateur ? Si tu as des choses à dire sur ce fil, dis-les dans ce fil pour que tout le monde puisse en profiter!

Pour aissayoub : je t'ai indiqué


As-tu calculé le premier morceau ? C'est bien sûr lui le plus intéressant dans la recherche d'un équivalent.
La question 1.5 sert pour majorer en module le deuxième morceau.

oui , le premier morceau c'est mais pour la majoration qu'est ce qu'on peut en déduire ?

[GaBuZoMeu]

1°) Peux-tu trouver un équivalent simple du premier morceau pour ?

2°) La majoration, comme je l'ai écrit ci-dessus, concerne le deuxième morceau.
Une fois ce deuxième morceau majoré, et une fois aussi le "troisième morceau" (l'intégrale à partir de ) également majoré, l'équivalent pour quand tombe tout seul.

[aissayoub]

1°) Peux-tu trouver un équivalent simple du premier morceau pour ?

2°) La majoration, comme je l'ai écrit ci-dessus, concerne le deuxième morceau.
Une fois ce deuxième morceau majoré, et une fois aussi le "troisième morceau" (l'intégrale à partir de ) également majoré, l'équivalent pour quand tombe tout seul.

1) oui , j'ai trouvé 1/2*ln(a)-ln(x)
2)comment on peut majoré le troisième morceau ?

[GaBuZoMeu]

1) moi je trouve . (se souvenir que est une constante ne dépendant pas de et que ).

2) La majoration du 3e morceau est un peu plus subtile. Je prends . On veut montrer que

est majoré en module par une constante ne dépendant pas de , comme le 2e morceau.
On se dit que ça ressemble beaucoup (d'autant plus que est plus petit) à la célèbre intégrale généralisée

Qu'à cela ne tienne, on écrit

et là ça devient facile.

[aissayoub]

1) j'ai pris a=1 pour que je puisse appliqué la question 1.5 , donc je trouve votre résultat.
2) avec l'astuce que vous avez écrit je trouve que le deuxième morceau tend vers 0 et le premier est dèja fini donc borné donc l'équivalence de "phi" est -i*ln(x).

P.S: je vois pas comment penser à l'astuce que vous avez utiliser pour prouver cette majoration.

[GaBuZoMeu]

De quelle "astuce" parles-tu ? Celle pour le "troisième morceau" ? J'ai essayé d'expliciter. On sait ce qu'il y a à faire : majorer par une constante indépendante de , et quand on regarde la tête de l'intégrale généralisée on ne peut pas s'empêcher de penser à celle de (enfin pour moi ça me semblait clair que c'était une bonne chose de s'y raccrocher).

[aissayoub]

d'accord, merci beaucoup !

[GaBuZoMeu]

Avec plaisir.

[aviateur]

On se dit que ça ressemble beaucoup (d'autant plus que est plus petit) à la célèbre intégrale généralisée

Heum! (pour reprendre tes expressions!) Dire que l'intégrale est "célèbre", je veux bien, mais pour un étudiant lambda, j'en suis moins sûr.
Mais en comparaison que dire d'un raisonnement si on évoque la célébrité de la série [1/n] (ou bien de [1/n^2]) sans préciser sa nature.

Je pense qu'il faut préciser que ta démonstration n'est valable que si on admet que l'intégrale est convergente.

Il y a tout de même une solution qui évite d'admettre ce résultat ci-dessus.

[GaBuZoMeu]

On n'admet rien, on démontre tout.
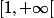
est l'exemple standard d'intégrale généralisée qui converge bien que la fonction ne soit pas intégrable sur l'intervalle . (Il y a des variantes avec ...)

Je rappelle la démonstration ultra classique, qui utilise l'intégration par parties :

suivie du passage à la limite , en utilisant que est bien intégrable sur .

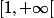
On ne coupera de toutes façons pas à un raisonnement qui fait intervenir une intégrale généralisée. Mais si tu as une autre façon de faire, vas-y, exprime toi ! Je trouve ça bizarre, d'être aussi grognon et de faire autant de cachotteries.

PS. Quand j'interviens pour aider quelqu'un, je n'ai pas l'habitude de tout expliciter, j'essaie de me limiter à des indications pour mettre sur la voie. Apparemment, la référence à cette intégrale généralisée qu'on trouve partout a suffi a aissayoub pour résoudre son exercice. Il faut croire qu'aissayoub n'est pas "un étudiant lambda". Tant mieux !