Lemme des noyaux !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 21 Jan 2009, 21:42
par barbu23 » 21 Jan 2009, 21:42
Bonsoir :
Soit

un espace vectoriel de dimension

sur un corps

. Soit :

un endomorphisme de

.
Soit :

avec :

et

sont premiers entre eux.
Alors :
 = \ker P_1(f) \oplus \ker P_2(f) $) Démonstration
Démonstration :
On a :

. D'après le théorème de Bézout, il existe
 \in (K[X])^2 $)
tel que

. On en déduit que
(f)=\mathrm{id}_E $)

désignant l'application identité de

).
Soit
 \cap \ker P_2(f) $)
. On a
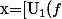 \circ P_1(f)](x)+[U_2(f) \circ P_2(f)](x)=0 $)
, donc
 \cap \ker P_2(f)=\{0\} $)
.
Soit
 $)
. On a alors
(f)](x)+[(U_2P_2)(f)](x) $)
. Or :
\{[(U_1P_1)(f)](x)\}=[(U_1P_1P_2)(f)](x)=[U_1(f) \circ P(f)](x)=0 $)
; ce qui montre que
(f)](x) \in \ker P_2(f) $)
. De même, on montre que
(f)](x) \in \ker P_1(f) $)
On en déduit donc que
 = \ker P_1(f) \oplus \ker P_2(f) $) Question
Question :
Le passage que 'ai pas compris est le suivant :
Or :
\{[(U_1P_1)(f)](x)\}=[(U_1P_1P_2)(f)](x)=[U_1(f) \circ P(f)](x)=0 $)
; ce qui montre que
(f)](x) \in \ker P_2(f) $)
. De même, on montre que
(f)](x) \in \ker P_1(f) $)
A quoi sert ce passage ? pour montrer quoi ?
Merci infiniment !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Jan 2009, 21:45
par Nightmare » 21 Jan 2009, 21:45
Salut :happy3:
On a écrit x, élement de KerP(f), comme la somme de [(U1P1)(f)](x) et de [(U2P2)(f)](x). Il suffit donc de montrer que le premier est dans Ker(P2(f)) et le second dans Ker(P1(f)) ce qui prouvera que KerP(f)=Ker(P1(f))+Ker(P2(f)).
Le premier paragraphe montre que la somme est directe.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 21 Jan 2009, 21:48
par barbu23 » 21 Jan 2009, 21:48
Merci beaucoup "Nightmare" pour ces precisions rapides ! :happy2:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Jan 2009, 21:49
par Nightmare » 21 Jan 2009, 21:49
Je t'en prie :happy3:
-
sniperamine
- Membre Relatif
- Messages: 366
- Enregistré le: 19 Jan 2009, 03:46
-
 par sniperamine » 21 Jan 2009, 22:00
par sniperamine » 21 Jan 2009, 22:00
ah c'est le théorème de décomposition de noyaux là tu veux le montrer pa récurrence :++:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 21 Jan 2009, 22:02
par barbu23 » 21 Jan 2009, 22:02
:zen: :zen: :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
; ce qui montre que
. De même, on montre que
; ce qui montre que
. De même, on montre que