Huhu

[totololo]

Bonsoir.
Je cherche des idées afin d'établir l'inégalité suivante :
Pour n élément de N , n! ;) exp(-n)(n+1)^n .

J'ai essayé de partir de n! ;) (n+1)^n que j'ai prouvé préalablement par récurrence, sans succès.
J'ai essayé d'étudier le signe de f(x)=n! - exp(-n)(n+1)^n , mais je ne sais pas dériver n! ni n^n.
J'ai essayé de transformer un petit peu l'expression pour faire apparaitre une fonction dérivable, mais sans succès.
Avez vous des idées qui pourraient me mettre sur une piste?
D'avance merci.

[girdav]

Je ne suis pas sûr de comprendre : si tu as montré que , tu pourrais conclure car . Le problème est que la première inégalité est fausse (tous les termes dans la factorielle sont plus petits que ).

[totololo]

Je ne suis pas sûr de comprendre : si tu as montré que , tu pourrais conclure car . Le problème est que la première inégalité est fausse (tous les termes dans la factorielle sont plus petits que ).

Toutes mes confuses ! Faute de frappe.
J'ai prouvé que (n+1)^n n!

[girdav]

As-tu essayé de montrer l'inégalité pour les logarithmes des deux membres?

[totololo]

As-tu essayé de montrer l'inégalité pour les logarithmes des deux membres?

Tu veux dire ln (n!) ln (exp(-n)(n+1)^n)?
EXCELENTE IDEE !
Je vais essayer sur le champ :p

[totololo]

CA MAAAARCHE !!!!!

Merci infiniment girdav !!! Tu gères !!!
=) =) =)

[totololo]

NON !!!!
On s'est planté -_-
On peut pas utiliser ln car cette fonction n'est pas définie en 0 et "n" appartient à N ...
Retour à la case départ.. Des idées? ^^

[girdav]

NON !!!!
On s'est planté -_-
On peut pas utiliser ln car cette fonction n'est pas définie en 0 et "n" appartient à N ...
Retour à la case départ.. Des idées? ^^

Je ne comprends pas ce que tu veux dire. On n'a pris à aucun moment le logarithme d'un truc nul. Et même si le truc était nul seulement pour , on aurait traité ce cas à part.

[totololo]

Je ne comprends pas ce que tu veux dire. On n'a pris à aucun moment le logarithme d'un truc nul. Et même si le truc était nul seulement pour , on aurait traité ce cas à part.

Donc il faut juste que je raisonne par disjonction des cas?
Je vérifie l'inégalité pour n=0;
J'utilise ln pour prouver l'inégalité pour n appartenant à N* .

[girdav]

Même pour aucun des termes intervenant dans l'inégalité est nul, donc je ne vois pas l'intérêt d'une telle disjonction.

[totololo]

Même pour aucun des termes intervenant dans l'inégalité est nul, donc je ne vois pas l'intérêt d'une telle disjonction.

Pour n=0 , n! = 0 => ln(n!) impossible

[girdav]

Je crois qu'il est convenu que .

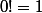
[totololo]

Je crois qu'il est convenu que .

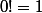
Ah ! :id:
Très juste...
Je réessaye de ce pas :p
Encore merci :we: