Graphe et nombres de chemins possibles
20 messages
- Page 1 sur 1
Graphe et nombres de chemins possibles
Soit G un graphe orienté, composé donc de points et de liaisons sous forme de flèches.
Je cherche à trouver une relation (une inégalité) entre le nombre de chemins possibles et le nombre de points et/ou le nombre de liaisons.
Il apparaît clairement quon ne peut bien minorer le nombre de chemins possibles : il est supérieur ou égal à 1 (on a égalité si on prend p points et p-1 liaisons, qui est le nombre minimal de liaisons pour relier les points entre eux et on obtient un graphe en forme de ver).
Je cherche donc une majoration du nombre de chemins possibles pour un graphe comportant p points et l liaisons.
Je donne quelques règles pour le tracer de graphe pour fixer le problème :
-On ne peut avoir de point isolé (tous doivent être reliés entre eux par au moins une liaison)
-Un chemin sarrête sil se termine par un point qui ne comporte par de liaisons descendante, ou sil repasse par un point qui appartient déjà à ce chemin (on ne tient pas compte des boucles, donc)
-Pour compter le nombre de chemins, on part dun point précis. Pour fixer les idées, ce sera le point à partir duquel commence le graphe, mais il ny aura pas forcément que des liaisons descendantes à partir de ce point, on peut imaginer quune boucle ramène au point de départ (et alors le chemin qui comprend cette boucle sarrête là, cf règle davant).
Après des tests, jai quelques remarques : jusquà 4 points, le nombre de chemins est inférieur ou égal au nombre de points -1 mais ensuite il le dépasse et croît sans doute assez vite.
Je pense quil faut faire appel à la combinatoire, les factorielles, les k parmi n mais jai du mal à voir comment. Je nai pas besoin dune majoration très précise (même si plus précis cela est, mieux cest) mais dune majoration tout du même.
Merci
Je cherche à trouver une relation (une inégalité) entre le nombre de chemins possibles et le nombre de points et/ou le nombre de liaisons.
Il apparaît clairement quon ne peut bien minorer le nombre de chemins possibles : il est supérieur ou égal à 1 (on a égalité si on prend p points et p-1 liaisons, qui est le nombre minimal de liaisons pour relier les points entre eux et on obtient un graphe en forme de ver).
Je cherche donc une majoration du nombre de chemins possibles pour un graphe comportant p points et l liaisons.
Je donne quelques règles pour le tracer de graphe pour fixer le problème :
-On ne peut avoir de point isolé (tous doivent être reliés entre eux par au moins une liaison)
-Un chemin sarrête sil se termine par un point qui ne comporte par de liaisons descendante, ou sil repasse par un point qui appartient déjà à ce chemin (on ne tient pas compte des boucles, donc)
-Pour compter le nombre de chemins, on part dun point précis. Pour fixer les idées, ce sera le point à partir duquel commence le graphe, mais il ny aura pas forcément que des liaisons descendantes à partir de ce point, on peut imaginer quune boucle ramène au point de départ (et alors le chemin qui comprend cette boucle sarrête là, cf règle davant).
Après des tests, jai quelques remarques : jusquà 4 points, le nombre de chemins est inférieur ou égal au nombre de points -1 mais ensuite il le dépasse et croît sans doute assez vite.
Je pense quil faut faire appel à la combinatoire, les factorielles, les k parmi n mais jai du mal à voir comment. Je nai pas besoin dune majoration très précise (même si plus précis cela est, mieux cest) mais dune majoration tout du même.
Merci
salut,
Je comprends pas ce qu'est une liaison descendante
Si on considère que par chemin tentends qu'on boucle pas et que tous les points du graphe appartiennent au chemin, alors
si on note) le nombre de chemins possibles pour n points.
le nombre de chemins possibles pour n points.
On peut prendre une chemin

On peut placer le n+1eme point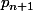 avant
avant  , apres
, apres  , ou entre deux points consécutifs.
, ou entre deux points consécutifs.
on a donc le nombre de placements de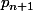 qui vaut
qui vaut 
On a donc
 = S(n) (n+1)!)
On s'arrete a n = 2, et S(2) = 1
Soit
 = \frac{n!}{2})
Un chemin sarrête sil se termine par un point qui ne comporte par de liaisons descendante
Je comprends pas ce qu'est une liaison descendante
Si on considère que par chemin tentends qu'on boucle pas et que tous les points du graphe appartiennent au chemin, alors
si on note
On peut prendre une chemin
On peut placer le n+1eme point
on a donc le nombre de placements de
On a donc
On s'arrete a n = 2, et S(2) = 1
Soit
la vie est une fête 
Je comprends pas ce qu'est une liaison descendante
On a un graphe orienté donc les liaisons sont sous la forme de flèches.
Exemple: 5->2->8
8 possède une liaison qui vient vers lui mais pas qui part de lui (et que j'appelle liaison descendante de 8).
En fait, on a un ensemble de points, reliés entre eux par des flèches, qui peuvent former des boucles ou pas (mais un chemin s'arrête dès qu'on retombe sur point déjà vu), on prend un de ces points, et on veut savoir combien on peut avoir de chemins différents à partir de ce point.
Dans l'exemple, on n'a qu'un seul chemin. 5->2->8->5 donne aussi un seul chemin (qui est 5,2,8 sinon ça ferait un chemin composé d'une infinité de points, en plus dans des cas plus complexes, de générer une infinité d'autres chemins).
Bien entendu un graphe normal n'est pas linéaire et là ça se corse... Jusqu'à quatre points, on peut majorer le nombre de chemins par nombre de points - 1, mais ensuite, le nombre de chemins possibles augmente trèès vite...
ben, jpense que jai fait ca.
Je rectifie par lexemple
Avec deux points A,B
A->B
Avec trois points A,B,C
A->B->C
A->C->B
Avec quatre points A,B,C,D
A->B->C->D
A->B->D->C
A->C->B->D
A->C->D->B
A->D->B->C
A->D->C->B
En partant toujours deA.
La formule si c'est lexemple que jdonne est correcte, c'est, en notant S(n) le nombre de chemins pour n points :
S(n) = (n-1)!
Pour compter le nombre de chemins, on part dun point précis
Je rectifie par lexemple
Avec deux points A,B
A->B
Avec trois points A,B,C
A->B->C
A->C->B
Avec quatre points A,B,C,D
A->B->C->D
A->B->D->C
A->C->B->D
A->C->D->B
A->D->B->C
A->D->C->B
En partant toujours deA.
La formule si c'est lexemple que jdonne est correcte, c'est, en notant S(n) le nombre de chemins pour n points :
S(n) = (n-1)!
la vie est une fête 
Merci de ta réponse, mais on continue de mal se comprendre. Le graphe est fixé, on cherche une loi sur le nombre de chemins possibles de n'importe quel graphe, bien souvent non linéaire.
http://www.hostingpics.net/viewer.php?id=572537Test_typeBIS.jpg
Ici par exemple 1-7-8-5 ou 1-7-9-10-12.
Je cherche une relation entre le nombre de liaisons et/ou le nombre de points et le nombre de chemins possibles. C'est difficile car à un graphe au nombre de points fixés, si on augmente le nombre de liaisons, le nombre de chemins n'augmente pas forcément (cf exemple juste après), donc on doit avoir une majoration large.
1
/ \
2 3
\ /
4
1
/ \ \
2 3 4
Dans le premier cas, 4 liaisons mais seulement deux chemins possibles. Dans le deuxième cas, 3 liaisons mais 3 chemins possibles.
http://www.hostingpics.net/viewer.php?id=572537Test_typeBIS.jpg
Ici par exemple 1-7-8-5 ou 1-7-9-10-12.
Je cherche une relation entre le nombre de liaisons et/ou le nombre de points et le nombre de chemins possibles. C'est difficile car à un graphe au nombre de points fixés, si on augmente le nombre de liaisons, le nombre de chemins n'augmente pas forcément (cf exemple juste après), donc on doit avoir une majoration large.
1
/ \
2 3
\ /
4
1
/ \ \
2 3 4
Dans le premier cas, 4 liaisons mais seulement deux chemins possibles. Dans le deuxième cas, 3 liaisons mais 3 chemins possibles.
Salut,
Il me semble que fatal_error te donne bien un majorant du nombre de chamin d'un graphe contenant n points. Comme il cherche un majorant ne dépendant que du nombre n de points (et pas du nombre d'arètes) il se place dans le "cas le pire" c'est à dire celui ou tout couples de points sont reliés par des arètes (dans les deux sens).
En relisant ton dernier post ou tu dit que dans le premier dessin, il y a seulement deux chemins possible, j'en déduit que pour toi, un chemin doit forcément se terminer par un "cul de sac" ou un "point déjà obtenu".
Me trompe-je ?
Il me semble que fatal_error te donne bien un majorant du nombre de chamin d'un graphe contenant n points. Comme il cherche un majorant ne dépendant que du nombre n de points (et pas du nombre d'arètes) il se place dans le "cas le pire" c'est à dire celui ou tout couples de points sont reliés par des arètes (dans les deux sens).
En relisant ton dernier post ou tu dit que dans le premier dessin, il y a seulement deux chemins possible, j'en déduit que pour toi, un chemin doit forcément se terminer par un "cul de sac" ou un "point déjà obtenu".
Me trompe-je ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
re,
merci pour le résumé ben.
Concernant
1
/ \
2 3
\ /
4
J'ai enfin compris! (enfin, je crois :marteau: )
Donc déjà, pour que le graphe soit connexe, si on a n points, il faut liaisons minimum.
liaisons minimum.
Donc pour n-1 liaisons, on peut faire n-1 chemins (en prenant le point 1, et en tirant un trait, 1 vers 2, 1 vers 3, 1 vers 4... etc) en faisant un truc "étoilé".
 = n-1) , avec
, avec  un graphe a n points et n-1 liaisons.
un graphe a n points et n-1 liaisons.
Ensuite, jvais noter) le nombre de culs de sacs pour un graphe a n points et n-1 liaisons.
le nombre de culs de sacs pour un graphe a n points et n-1 liaisons.
L'idée c'est déjà de montrer que le nombre de chemins, c'est le nombre de culs de sacs.
Prenons q un cul de sac quelconque.
Tous les chemins menent au q.
Maintenant faut voir que ya pas de q seul.
Si un q n'est dans aucun chemin, ca veut dire que son parent (il en a forcément un vu que le graphe est connexe) n'appartient pas un chemin. (rappel: )
)
De fait, le parent du parent non plus (en evitant les cycles). Et le parent n'est jamais 1 (qui debute le chemin)(sinon, on a un cycle). Donc on passe jamais par 1. Donc le sous-graphe auquel on appartient est pas "attaché" un sous-graphe qui contient 1. Absurde, donc q appartient a un chemin.
mm un peu bancal, mais jpense que c'est juste.
Bref, le nombre de chemins c'est le nombre de culs de sac.
On a montré que = C(G_{n,n-1})=n-1)
Maintenant, si on prend l = n, on rajoute une liaison.
En prenant le graphe a n points, on veut minimiser le retrait de culs de sac.
Ici, il faut montrer que en ajoutant une liaison dans notre graphe qu'on considère "celui qui donne le plus de chemins", que celui-ci soit toujours celui qui en offre le plus (qu'un autre graphe qui a initialement moins de culs de sac, mais si on ajoute des liaisons, il en offre pas plus que le notre). Mais jvois pas comment.
Donc >>>>>>>>>hypothèse(de boeuf)=3 \text{ et }P(2) = 2[/TEX]
On a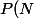 = 2(N-2)+1+P(N-1))
qui nous mene a
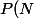 = (N-2)N+2)
Nous on veut plutot le nombre de q perdus pour l liaisons cad la "bijection" de P (spa vraiment une bij, mais dans l'idée d'inverser)
On passe dans R, et on veut inverser

soit
pour = 5\text{ et }x \geq 0)
si on note L(l) le nombre de culs perdus pour l liaisons, on a alors
 = 1 + E(\sqrt{l - 1})\\<br />l=1 \Rightarrow L(1) = 1\\<br />l\in [ 2;4 ] \Rightarrow L(l) = 2)
BREF XD
 = n-1 - L(l-(n-1)))
Et la jme dis que si mon hypo elle est fausse, c'est ballo lol
merci pour le résumé ben.
Concernant
1
/ \
2 3
\ /
4
J'ai enfin compris! (enfin, je crois :marteau: )
Donc déjà, pour que le graphe soit connexe, si on a n points, il faut
Donc pour n-1 liaisons, on peut faire n-1 chemins (en prenant le point 1, et en tirant un trait, 1 vers 2, 1 vers 3, 1 vers 4... etc) en faisant un truc "étoilé".
Ensuite, jvais noter
L'idée c'est déjà de montrer que le nombre de chemins, c'est le nombre de culs de sacs.
Prenons q un cul de sac quelconque.
Tous les chemins menent au q.
Maintenant faut voir que ya pas de q seul.
Si un q n'est dans aucun chemin, ca veut dire que son parent (il en a forcément un vu que le graphe est connexe) n'appartient pas un chemin. (rappel:
De fait, le parent du parent non plus (en evitant les cycles). Et le parent n'est jamais 1 (qui debute le chemin)(sinon, on a un cycle). Donc on passe jamais par 1. Donc le sous-graphe auquel on appartient est pas "attaché" un sous-graphe qui contient 1. Absurde, donc q appartient a un chemin.
mm un peu bancal, mais jpense que c'est juste.
Bref, le nombre de chemins c'est le nombre de culs de sac.
On a montré que
Maintenant, si on prend l = n, on rajoute une liaison.
En prenant le graphe a n points, on veut minimiser le retrait de culs de sac.
Ici, il faut montrer que en ajoutant une liaison dans notre graphe qu'on considère "celui qui donne le plus de chemins", que celui-ci soit toujours celui qui en offre le plus (qu'un autre graphe qui a initialement moins de culs de sac, mais si on ajoute des liaisons, il en offre pas plus que le notre). Mais jvois pas comment.
Donc >>>>>>>>>hypothèse(de boeuf)=3 \text{ et }P(2) = 2[/TEX]
On a
qui nous mene a
Nous on veut plutot le nombre de q perdus pour l liaisons cad la "bijection" de P (spa vraiment une bij, mais dans l'idée d'inverser)
On passe dans R, et on veut inverser
soit
pour
si on note L(l) le nombre de culs perdus pour l liaisons, on a alors
BREF XD
Et la jme dis que si mon hypo elle est fausse, c'est ballo lol
la vie est une fête 
« En relisant ton dernier post ou tu dit que dans le premier dessin, il y a seulement deux chemins possible, j'en déduit que pour toi, un chemin doit forcément se terminer par un "cul de sac" ou un "point déjà obtenu".
Me trompe-je ? »
Tout juste.
Merci beaucoup, je vais lire ça à tête reposée. Ceci dit, je me demande si fatal_error na pas fait la même erreur que moi au départ, quand je pensais que le monde était beau et gentil : le nombre maximal de chemins serait le nombre de culs de sac. Cest vrai seulement pour un petit nombre de points, comme 4 ou 5. Après ça foire.
Prenons le graphe que je vous ai envoyé : si on prend la partie à droite, en prenant les points 1, 8, 9, 10, 5 et 12, on a bien 4 chemins possibles pour 6 points, ce qui est inférieur à 6-1 le nombre maximal de culs de sac pour 6 points.
Mais à gauche (points 1,3,4,11,2,6,12), on a 1-3-6-12, 1-3-6-4-12, 1-3-6-4-2 (le chemin revient au 6, donc on sarrête), 1-3-6-4-2-12, 1-3-4-12 facilement une vingtaine (même si on n'avait pas la boucle). Le nombre de chemin augmente de manière exponentielle quand on augmente le nombre de paragraphe et qu'on a beaucoup de liaisons. Il doit y avoir un n! dans le majorant...
Me trompe-je ? »
Tout juste.
Merci beaucoup, je vais lire ça à tête reposée. Ceci dit, je me demande si fatal_error na pas fait la même erreur que moi au départ, quand je pensais que le monde était beau et gentil : le nombre maximal de chemins serait le nombre de culs de sac. Cest vrai seulement pour un petit nombre de points, comme 4 ou 5. Après ça foire.
Prenons le graphe que je vous ai envoyé : si on prend la partie à droite, en prenant les points 1, 8, 9, 10, 5 et 12, on a bien 4 chemins possibles pour 6 points, ce qui est inférieur à 6-1 le nombre maximal de culs de sac pour 6 points.
Mais à gauche (points 1,3,4,11,2,6,12), on a 1-3-6-12, 1-3-6-4-12, 1-3-6-4-2 (le chemin revient au 6, donc on sarrête), 1-3-6-4-2-12, 1-3-4-12 facilement une vingtaine (même si on n'avait pas la boucle). Le nombre de chemin augmente de manière exponentielle quand on augmente le nombre de paragraphe et qu'on a beaucoup de liaisons. Il doit y avoir un n! dans le majorant...
Langue au chat?
Je rappelle qu'on part d'un point d'un graphe quelconque, et qu'on cherche à majorer le nombre de chemins qu'on peut parcourir à partir de ce point sans passer deux fois par le même point.
Le majorant contient sans doute le nombre de liaisons et le nombre de points. Il faut utiliser la combinatoire je pense, avec des factorielles, des coefficients binomiaux, mais je bloque toujours...
Je rappelle qu'on part d'un point d'un graphe quelconque, et qu'on cherche à majorer le nombre de chemins qu'on peut parcourir à partir de ce point sans passer deux fois par le même point.
Le majorant contient sans doute le nombre de liaisons et le nombre de points. Il faut utiliser la combinatoire je pense, avec des factorielles, des coefficients binomiaux, mais je bloque toujours...
re,
jai un peu réfléchi au truc, mais ca m'a saoulé, donc jte donne les qq pistes sur lesquelles chui parti, mais c'est pas non plus exceptionnel...
Donc déjà, on note n le nombre de noeuds
l le nombre de liaisons libres, cad pour reliés n noeuds, il faut n-1 liaisons. Chaque liaison supplémentaire est comptée. Donc si on a n liaison, l = 1, n+1 liaisons, l = 2, etc...
On note C(n,l) le nombre de chemins pour n noeuds et l liaisons supplémentaires.
Pour l = 0, il est clair que le nombre max de chemins, c'est n-1. On fait un truc étoilé

C(n,0) = n-1
Pour l = 1, on met tous les culs de sacs dans le même noeud Q, et on sort un noeud Q' auquel on rajoute une liaison Q'Q pour factoriser les chemins passant par Q.

C(n,1) = max[(((n-1)-1) -1)*2 = 2n - 6; (n-1)- 1 = n-2]
Pour l = 2, ca dépend.

Dans le premier cas, on considère qu'on a une optimale, et on se contente de rajouter un chemin. Mais on peut aussi tenter de factoriser... donc là, on a
C(n,2) = max[((n-2)-l)*(l+1); C(n,1)+1 = n-1]
ici, c'est avec pincettes, parce que ca dépend du nombre de culs de sacs factorisés.
On peut remarquer dans l'image suivante

que rajouter un noeud dans une arrete ne sert a rien, il vaut mieux factoriser
La même pour trois liaisons

Une fois qu'on a remonté un noeud, ya plus besoin de remonter les autres, on peut rajouter des liaisons dans " l'étage du dessus " pour factoriser au maximum.
Enfin, jme suis donc arreté là :

On essaie de compléter au maximum les étages supérieurs, pis après, rebelote : il faut choisir entre passer un noeud dans l'étage supérieur ou refaire la même chose dans l'étage inférieur où on a "déplacé" notre noeud Init.
jai un peu réfléchi au truc, mais ca m'a saoulé, donc jte donne les qq pistes sur lesquelles chui parti, mais c'est pas non plus exceptionnel...
Donc déjà, on note n le nombre de noeuds
l le nombre de liaisons libres, cad pour reliés n noeuds, il faut n-1 liaisons. Chaque liaison supplémentaire est comptée. Donc si on a n liaison, l = 1, n+1 liaisons, l = 2, etc...
On note C(n,l) le nombre de chemins pour n noeuds et l liaisons supplémentaires.
Pour l = 0, il est clair que le nombre max de chemins, c'est n-1. On fait un truc étoilé

C(n,0) = n-1
Pour l = 1, on met tous les culs de sacs dans le même noeud Q, et on sort un noeud Q' auquel on rajoute une liaison Q'Q pour factoriser les chemins passant par Q.

C(n,1) = max[(((n-1)-1) -1)*2 = 2n - 6; (n-1)- 1 = n-2]
Pour l = 2, ca dépend.

Dans le premier cas, on considère qu'on a une optimale, et on se contente de rajouter un chemin. Mais on peut aussi tenter de factoriser... donc là, on a
C(n,2) = max[((n-2)-l)*(l+1); C(n,1)+1 = n-1]
ici, c'est avec pincettes, parce que ca dépend du nombre de culs de sacs factorisés.
On peut remarquer dans l'image suivante

que rajouter un noeud dans une arrete ne sert a rien, il vaut mieux factoriser
La même pour trois liaisons

Une fois qu'on a remonté un noeud, ya plus besoin de remonter les autres, on peut rajouter des liaisons dans " l'étage du dessus " pour factoriser au maximum.
Enfin, jme suis donc arreté là :

On essaie de compléter au maximum les étages supérieurs, pis après, rebelote : il faut choisir entre passer un noeud dans l'étage supérieur ou refaire la même chose dans l'étage inférieur où on a "déplacé" notre noeud Init.
la vie est une fête 
Dans mes exemples il n'y a pas souvent en moyenne plus de deux liaisons par point (le maximal que j'ai est 2.2 environ, donc au pire l=2.2*n - (n-1) soit lmax=1.2n+1 ) avec n valant plusieurs centaines quand même donc j'ai intérêt à trouver une loi générale je crois.
Enfin il faut que je reprenne ça l'esprit un peu plus clair. Merci beaucoup pour tes efforts :fan:
Enfin il faut que je reprenne ça l'esprit un peu plus clair. Merci beaucoup pour tes efforts :fan:
En fait, jai du mal à comprendre comment tu trouves :
C(n,1) = max[(((n-1)-1) -1)*2 = 2n - 6; (n-1)- 1 = n-2]
(On peut dailleurs, vu que le nombre de points sera supérieur à 4, enlever le max et prendre juste 2n 6.)
"On essaie de compléter au maximum les étages supérieurs, pis après, rebelote "
C'est quoi le maximum?
C(n,1) = max[(((n-1)-1) -1)*2 = 2n - 6; (n-1)- 1 = n-2]
(On peut dailleurs, vu que le nombre de points sera supérieur à 4, enlever le max et prendre juste 2n 6.)
"On essaie de compléter au maximum les étages supérieurs, pis après, rebelote "
C'est quoi le maximum?
J'ai une autre remarque, toujours dans les graphes orientés.
Imaginons qu'un ait une matrice d'adjacence (avec des 0 et des 1, les 1 indiquant les liaisons) qui représente un graphe orienté sans boucle. Alors elle est nilpotente et son indice de nilpotence est la taille du chemin maximal + 1, c'est-à-dire que l'indice nilpotence est égal au nombre de liaisons + 1 du chemin de longueur maximal.
Ceci dit, dès qu'on a une boucle, ça ne marche plus, les puissances de matrice font des "boucles" elles aussi (si A²=B, A^3=C, A^4=D, A^5=E, A^6=C on aura pour certaines boucles B,C,D,E,C,D,E...
Donc ce sera inapplicable à mes graphes qui ont tout le temps des boucles.
En revanche, j'aimerai bien savoir si ce que j'ai dit pour un graphe sans boucle est juste, si ce résultat est largement connu...
Imaginons qu'un ait une matrice d'adjacence (avec des 0 et des 1, les 1 indiquant les liaisons) qui représente un graphe orienté sans boucle. Alors elle est nilpotente et son indice de nilpotence est la taille du chemin maximal + 1, c'est-à-dire que l'indice nilpotence est égal au nombre de liaisons + 1 du chemin de longueur maximal.
Ceci dit, dès qu'on a une boucle, ça ne marche plus, les puissances de matrice font des "boucles" elles aussi (si A²=B, A^3=C, A^4=D, A^5=E, A^6=C on aura pour certaines boucles B,C,D,E,C,D,E...
Donc ce sera inapplicable à mes graphes qui ont tout le temps des boucles.
En revanche, j'aimerai bien savoir si ce que j'ai dit pour un graphe sans boucle est juste, si ce résultat est largement connu...
En fait, jai du mal à comprendre comment tu trouves :
C(n,1) = max[(((n-1)-1) -1)*2 = 2n - 6; (n-1)- 1 = n-2]
On enlève le noeud init, on enlève un chemin : n-1
On a le noeud Q qui factorise les Q de sacs, donc il constitue pas "un chemin". On enlève un chemin : (n-1)-1
On enleve un noeud Q' des culs de sacs et on le remonte à hauteur de Q. On enlève un autre chemin. ((n-1)-1)-1
On factorise ce nombre de chemin, l'un passe par Q, l'autre par Q', donc [((n-1)-1)-1]*2
"On essaie de compléter au maximum les étages supérieurs, pis après, rebelote "
C'est quoi le maximum?
fallait comprendre le plus que possible, ie j'ai pas tenté de calculer...
Par contre, le max jpense qu'il faut le garder parce que quand on arrive a un nombre de liaisons importantes, i faut plus retirer des culs de sacs (on perd les "atouts" de factorisation), et i vaut mieux tirer une liaison vers l'étage du dessous...
la vie est une fête 
Alors elle est nilpotente et son indice de nilpotence est la taille du chemin maximal + 1, c'est-à-dire que l'indice nilpotence est égal au nombre de liaisons + 1 du chemin de longueur maximal.
Si A est la matrice d'adjacence,
alors A^2 représente les nombres de chemins de longueur 2 d'un noeud vers l'autre.
Donc A^k les chemins de longueur k, et si il existe pas de chemins de longueur k+1, alors A^{k+1} est nulle, de faite A est nilpotente d'indice k+1.
Il faut pe démontrer que A^k représente les chemins de longueur k...
voilà un lien
la vie est une fête 
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
