Bonsoir,
je trouve sur wiki qu'on peut démontrer la formule du crible à l'aide la fonction indicatrice .
comment on procède ?
Merci
Formule de crible
4 messages
- Page 1 sur 1
par Nightmare » 30 Sep 2007, 18:57
Bonsoir :happy3:
Je l'ai eu en DS, voici comment j'ai procédé :
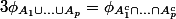^{c}}=1-(1-\phi_{A_{1}})...(1-\phi_{A_{p}}))
Si on développe le produit, chaque terme de la somme sera un produit de p termes, donc chacun est soit 1, soit du type
. Le produit vaut donc ^{Card(J)}\Bigprod_{j\in J} \phi_{A_{j}})
Pour J vide, le produit vaut 1.
On a donc...(1-\phi_{A_{p}})=1-\Bigsum_{J\subset [|1,p|]} (-1)^{card(J)}\Bigprod_{j\in J} \phi_{A_{j}}\;\;=\;\;\Bigsum_{J\subset [|1,p|], J\no=\empty} (-1)^{card(J)-1} \Bigprod_{j\in J} \phi_{A_{j}})
:happy3:
Je l'ai eu en DS, voici comment j'ai procédé :
Si on développe le produit, chaque terme de la somme sera un produit de p termes, donc chacun est soit 1, soit du type
Pour J vide, le produit vaut 1.
On a donc
:happy3:
par SimonB » 01 Oct 2007, 06:43
Plus joli si l'on veut, mais ce que j'ai eu, c'était un joli exercice où l'on démontrait tout sur l'indicatrice d'Euler... à partir de la formule du crible ! ;) Je trouve ça aussi très joli...
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :