Faisceau
39 messages
- Page 2 sur 2 - 1, 2
@mathelot : je ne peux que conseiller le très bon livre de Hartshorne "Algebraic Geometry" (et surtout de le méditer très longuement, parce qu'il y a ce qu'il dit et ce qu'il ne dit pas)
Pour ce qui est de la fibre O_{X,x}, il s'agit d'un localisé en un idéal premier p pour un schéma affine X = Spec A, et je crois que c'est comme ça qu'il faut le voir pour n'importe quel schéma (ne pas oublier qu'un schéma quelconque est par définition un collage de schémas affines). Les opérations de restriction du type O_X(U) -> O_{X,x} sont alors simplement vues comme des localisations A -> A_p (on commence par restreindre U à un ouvert affine, qui forment une base de la topologie du schéma).
Bien sur ça ne fonctionne que si on parle de "schémas", et pas simplement d'espaces annelés.
Pour ce qui est de la fibre O_{X,x}, il s'agit d'un localisé en un idéal premier p pour un schéma affine X = Spec A, et je crois que c'est comme ça qu'il faut le voir pour n'importe quel schéma (ne pas oublier qu'un schéma quelconque est par définition un collage de schémas affines). Les opérations de restriction du type O_X(U) -> O_{X,x} sont alors simplement vues comme des localisations A -> A_p (on commence par restreindre U à un ouvert affine, qui forment une base de la topologie du schéma).
Bien sur ça ne fonctionne que si on parle de "schémas", et pas simplement d'espaces annelés.
Perso, un article, avant de lire "le bas" comme tu dit, j'ai tendance à commencer par "le haut" et là, comme par hasard, ça commence par un "...on discrete topology ..." donc se place dans le cas où les singletons {x} sont des ouverts (ce qui ne me semble pas vraiment être le cas le plus passionnant d'espace topologique...  )
)
Et sinon, si tu regarde ta définition de "fibré", par limite inductive, tu vois bien qu'il y ait fait référence à l'ensemble des ouverts contenant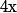 et que c'est tout autant une définition locale que celle avec la relation d'équivalence (et pas une définition ponctuelle)
et que c'est tout autant une définition locale que celle avec la relation d'équivalence (et pas une définition ponctuelle)
Donc je le redit : comme tout ce qui est propriété (ou définition) locale, tu ne risque pas de voir comment ça marche avec uniquement la connaissance de ce qui se passe au point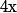 (sauf si le singleton {x} est ouvert bien entendu, mais dans ce cas, il n'y a plus besoin de limite inductive non plus !!!)
(sauf si le singleton {x} est ouvert bien entendu, mais dans ce cas, il n'y a plus besoin de limite inductive non plus !!!)
Et sinon, si tu regarde ta définition de "fibré", par limite inductive, tu vois bien qu'il y ait fait référence à l'ensemble des ouverts contenant
Donc je le redit : comme tout ce qui est propriété (ou définition) locale, tu ne risque pas de voir comment ça marche avec uniquement la connaissance de ce qui se passe au point
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Perso, un article, avant de lire "le bas" comme tu dit, j'ai tendance à commencer par "le haut" et là, comme par hasard, ça commence par un "...on discrete topology ..." donc se place dans le cas où les singletons {x} sont des ouverts (ce qui ne me semble pas vraiment être le cas le plus passionnant d'espace topologique...  )
)
Et sinon, si tu regarde ta définition de "fibré", par limite inductive, tu vois bien qu'il y ait fait référence à l'ensemble des ouverts contenant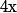 et que c'est tout autant une définition locale que celle avec la relation d'équivalence (et pas une définition ponctuelle)
et que c'est tout autant une définition locale que celle avec la relation d'équivalence (et pas une définition ponctuelle)
Donc je le redit : comme tout ce qui est propriété (ou définition) locale, tu ne risque pas de voir comment ça marche avec uniquement la connaissance de ce qui se passe au point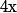 (sauf si le singleton {x} est ouvert bien entendu, mais dans ce cas, il n'y a plus besoin de limite inductive non plus !!!)
(sauf si le singleton {x} est ouvert bien entendu, mais dans ce cas, il n'y a plus besoin de limite inductive non plus !!!)
Et sinon, si tu regarde ta définition de "fibré", par limite inductive, tu vois bien qu'il y ait fait référence à l'ensemble des ouverts contenant
Donc je le redit : comme tout ce qui est propriété (ou définition) locale, tu ne risque pas de voir comment ça marche avec uniquement la connaissance de ce qui se passe au point
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
Juste une petite remarque : je n'y connait absolument que dalle en "faisceaux", mais vu la définition que tu donne du fibréavec ton quotient de
, j'ai un tout petit peu l'impression que pour que
ait du sens, y'aurais comme qui dirait intérêt à ce que
soit un ouvert.
Donc tes, je pense que ça risque pas d'avoir beaucoup de sens, et si par hasard ça en as un, ça m'étonnerais profondément que ça ait quelque chose à voir avec
qui, par définition, dépend de ce qui se passe au voisinage de
et pas uniquement de ce qui se passe au point
.
C'est un peu comme si tu voulais définir la dérivée f'(xo) en un point xo en ne connaissant que la valeur de f(xo) : ça risque pas de suffire...
tu peux mieux expliquer , on n'y comprend rien.
Dans ce contexte, moi aussi j'y connais "que dalle", il a été dit que toutes les topologies étaient triviales.
@L.A. : merci pour la référence.
C'est un peu comme si tu voulais définir la dérivée f'(xo) en un point xo en ne connaissant que la valeur de f(xo) : ça risque pas de suffire...
Je dirais plutôt que le germe correspond à un développement en série au voisinage d'un point pour une fonction holomorphe, ce qui est loin d'être équivalent à la valeur de la fonction en ce point. Et d'ailleurs les schémas intègres vérifient aussi un "principe de prolongement analytique" : si deux sections ont le même germe en un point alors elles coïncident sur l'intersection de leurs ouverts de définition, et se recollent donc en une seule section.
Rmq : Le "développement en série" se lit dans le germe O_{X,x}, la "valeur en un point" se lit dans le corps résiduel k(x) = O_{X,x}/m_x.
Ben314 a écrit:Perso, un article, avant de lire "le bas" comme tu dit, j'ai tendance à commencer par "le haut" et là, comme par hasard, ça commence par un "...on discrete topology ..." donc se place dans le cas où les singletons {x} sont des ouverts (ce qui ne me semble pas vraiment être le cas le plus passionnant d'espace topologique...)
Et sinon, si tu regarde ta définition de "fibré", par limite inductive, tu vois bien qu'il y ait fait référence à l'ensemble des ouverts contenantet que c'est tout autant une définition locale que celle avec la relation d'équivalence (et pas une définition ponctuelle)
Donc je le redit : comme tout ce qui est propriété (ou définition) locale, tu ne risque pas de voir comment ça marche avec uniquement la connaissance de ce qui se passe au point(sauf si le singleton {x} est ouvert bien entendu, mais dans ce cas, il n'y a plus besoin de limite inductive non plus !!!)
Tu as raison @Ben il me semble. :happy3:
En fait, si
Pour moi, les éléments de
Merci d'avance.
NON, c'est FAUX : on a bien une suites d'éléments 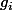 pour i entier (en considérant qu'on est dans un cas où le point x admet un système fondamental dénombrable de voisinage), mais IL N'Y A PAS d'élément du style de ton
pour i entier (en considérant qu'on est dans un cas où le point x admet un système fondamental dénombrable de voisinage), mais IL N'Y A PAS d'élément du style de ton  pour une raison évidente :
pour une raison évidente :  n'est en général pas ouvert, mais réduit à {x}.
n'est en général pas ouvert, mais réduit à {x}.
D'où, bis et répétita, tu ne résumera en général pas l'information contenu dans ta limite inductive a l'aide d'un unique élément.
Et en ce qui concerne le "ça représente quoi", ben c'est la même chose que tout ce que l'on construit en math. par quotient à l'aide d'une relation d'équivalence : pour définir un nouveau "concept", on regroupe les éléments en "classe" d'éléments qui on une propriété commune.
C'est comme ça qu'on construit Z (partant de N), Q (partant de Z), Z/nZ (partant de Z), R (partant de Q), les espaces Lp (avec un L), etc...
D'où, bis et répétita, tu ne résumera en général pas l'information contenu dans ta limite inductive a l'aide d'un unique élément.
Et en ce qui concerne le "ça représente quoi", ben c'est la même chose que tout ce que l'on construit en math. par quotient à l'aide d'une relation d'équivalence : pour définir un nouveau "concept", on regroupe les éléments en "classe" d'éléments qui on une propriété commune.
C'est comme ça qu'on construit Z (partant de N), Q (partant de Z), Z/nZ (partant de Z), R (partant de Q), les espaces Lp (avec un L), etc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonsoir à tous, :happy3:
@L.A. : Il y'a un passage de mon cours qui se rapproche de ce que tu dis, mais sans démonstration, peux tu me donner sa démonstration, ou me clarifier pourquoi ? Le voici ce passage :
Soit un espace topologique. Si
un espace topologique. Si  , et si
, et si  est l'origine et que
est l'origine et que 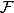 est le préfaisceau des fonctions holomorphes, alors, la fibre
est le préfaisceau des fonctions holomorphes, alors, la fibre  s'identifie à la
s'identifie à la  - algèbre :
- algèbre :  des séries formelles en
des séries formelles en  de rayon
de rayon 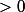 .
.
Merci d'avance. :happy3:
L.A. a écrit: ... le germe correspond à un développement en série au voisinage d'un point pour une fonction holomorphe, ce qui est loin d'être équivalent à la valeur de la fonction en ce point. Et d'ailleurs les schémas intègres vérifient aussi un "principe de prolongement analytique" : si deux sections ont le même germe en un point alors elles coïncident sur l'intersection de leurs ouverts de définition, et se recollent donc en une seule section.
.
@L.A. : Il y'a un passage de mon cours qui se rapproche de ce que tu dis, mais sans démonstration, peux tu me donner sa démonstration, ou me clarifier pourquoi ? Le voici ce passage :
Soit
Merci d'avance. :happy3:
Ici il suffit (entre guillemets) d'utiliser la définition du germe en termes de limite inductive.
Si U est un ouvert de C contenant x, tu as un morphisme naturel de C-algèbres : F(U) -> C{z} (rmq : je ne connais pas cette notation) qui à un fonction holomorphe f sur U associe la série formelle qui correspond à sont développement en x (celle ci a bien un rayon de convergence > 0 puisque f est définie sur un voisinage de x).
En outre, si f ~ g ont même germe en x (c'est à dire coincident dans F_x, c'est à dire qu'il existe un ouvert V contenant x assez petit tel que f|V = g|V) alors leur image dans C{z} est la même. Le morphisme passe donc au quotient par ~ et définit un morphisme F_x -> C{z}. Il ne reste plus qu'à prouver que c'est un isomorphisme, je te le laisse.
Si U est un ouvert de C contenant x, tu as un morphisme naturel de C-algèbres : F(U) -> C{z} (rmq : je ne connais pas cette notation) qui à un fonction holomorphe f sur U associe la série formelle qui correspond à sont développement en x (celle ci a bien un rayon de convergence > 0 puisque f est définie sur un voisinage de x).
En outre, si f ~ g ont même germe en x (c'est à dire coincident dans F_x, c'est à dire qu'il existe un ouvert V contenant x assez petit tel que f|V = g|V) alors leur image dans C{z} est la même. Le morphisme passe donc au quotient par ~ et définit un morphisme F_x -> C{z}. Il ne reste plus qu'à prouver que c'est un isomorphisme, je te le laisse.
Bonjour @L.A. , :happy3:
Sauf erreur, tu es parti du morphisme \to \mathbb{C} \{ z \}) défini par :
défini par :  = \displaystyle \sum_{n \geq 0} \dfrac{g^{(n)} (0) }{n!} z^n) , non ? Il me semble que c'est un morphisme surjective, car si on prend une série formelle de rayon de convergence
, non ? Il me semble que c'est un morphisme surjective, car si on prend une série formelle de rayon de convergence 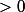 , de la forme :
, de la forme :  , alors : il existe un
, alors : il existe un ) avec
avec  contient le domaine de convergence de la série formelle, tel que :
contient le domaine de convergence de la série formelle, tel que : } (0)}{n!}) ,non ? Si c'est vrai ce que j'ai dit, cela signifie que
,non ? Si c'est vrai ce que j'ai dit, cela signifie que  est surjective.
est surjective.
On pose : = f(g) = \displaystyle \sum_{n \geq 0} \dfrac{g^{(n)} (0) }{n!} z^n) , et donc,
, et donc, 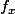 est aussi surjective par construction. ( Même raisonnement que çi - dessus ). Correct ?
est aussi surjective par construction. ( Même raisonnement que çi - dessus ). Correct ?
Pour l'injectivité, attend, je vais y réflechir. :happy3:
Edit : Pour l'injectivité, soit : tel que
tel que  = f(g) = 0 = \displaystyle \sum_{n \geq 0} \dfrac{g^{(n)} (0) }{n!} z^n) , cela signifie que :
, cela signifie que :  et
et 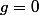 , et par conséquent :
, et par conséquent :  , non ? d'où l'injectivité.
, non ? d'où l'injectivité.
Merci d'avance. :happy3:
Sauf erreur, tu es parti du morphisme
On pose :
Pour l'injectivité, attend, je vais y réflechir. :happy3:
Edit : Pour l'injectivité, soit :
Merci d'avance. :happy3:
Oui, pour la surjectivité, on sait que n'importe quelle série entière de rayon >0 définit une fonction holomorphe sur le disque correspondant, donc à partir d'une série il est facile de construire une fonction et de prendre son germe.
Pour l'injectivité, si f(g)=0 ça veut dire que le développement de g est la série formelle nulle, donc il existe un disque V tel que g|V = 0 = 0|V, et donc g_x = 0_x.
Tu peux remarquer que tout ça est vraiment lourd comme preuve, quoiqu'on fasse on a l'impression de tourner en rond, c'est pour ça qu'on a raison de s'autoriser à l'omettre de temps en temps...
Pour l'injectivité, si f(g)=0 ça veut dire que le développement de g est la série formelle nulle, donc il existe un disque V tel que g|V = 0 = 0|V, et donc g_x = 0_x.
Tu peux remarquer que tout ça est vraiment lourd comme preuve, quoiqu'on fasse on a l'impression de tourner en rond, c'est pour ça qu'on a raison de s'autoriser à l'omettre de temps en temps...
Bonsoir à tous, :happy3:
Pourriez vous svp m'expliquer pourquoi :) comme ça a été dit ici : http://www.les-mathematiques.net/phorum/read.php?3,1014419 dans le message de GaBuZoMeu. ? Il affirme que :
comme ça a été dit ici : http://www.les-mathematiques.net/phorum/read.php?3,1014419 dans le message de GaBuZoMeu. ? Il affirme que : ) est une injection canonique.
est une injection canonique.
Merci d'avance. :happy3:
Pourriez vous svp m'expliquer pourquoi :
Merci d'avance. :happy3:
39 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
