Étude de xarctan(1/x)

[Amoroth]

Bonjour à tous,
Je cherche à comprendre pourquoi la limite de x*arctan(1/x) lorsque x tend vers +00 est égale à 1 alors que limite de arctan(1/x) lorsque x tend vers +00 est égale à 0
Merci de votre aide

[Pseuda]

Bonjour,

C'est normal, ce n'est pas la même fonction ...

Avec la composition des limites, 1/x -> 0 quand x -> +oo, et arctan t -> 0 quand t -> 0 (en posant t=1/x).

Pour x arctan (1/x) = arctan (1/x) / (1/x), on peut poser aussi 1/x = t, et le DL1 en 0 de arctan t = t + t o(1), donc :
(arctan t) / t = 1 + o(1) -> 1

[Amoroth]

Bonjour, merci pour la réponse
Seulement je n'ai pas compris...
Pouvez-vous développez le calcul de la limite de xarctan(1/x)?
DL1=Développement limité à l'ordre 1?
Merci d'avance

[Pseuda]

Bonjour,

Reprenons. Oui, DL1 = développement limité à l'ordre 1.

On a : lim arctan(1/x) = 0 quand x -> +oo, donc lim x * arctanx est une forme indéterminée (+oo * 0).

On fait donc un changement de variable t = 1/x, et cela revient à calculer la limite de (arctan t)/t quand t -> 0.

Or, comme arctan t = t + t o(1) (DL1 en 0 de la fonction arctan), alors arctan t = (t +t o(1)) / t = 1 + o(1), avec o(1) fonction qui tend vers 0 avec t. Donc x arctan (1/x) = (arctan t) / t -> 1.

Tu peux aussi utiliser les équivalents et dire que : arctan t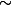 t en 0 (arctan t) / t -> ?

[Amoroth]

Merci j'y vois plus clair...
ce qui m’étonne c'est que l'on a pas encore vu ça en cours...
Il y a peut être une autre façon de faire que l’étude de cette limite...

Je devais simplifier l'expression de f(x)=arctanx+arctan(1/x)
Ensuite il faut montrer que g(x)=xarctan(x) admet une asymptote d'équation y= x(pi/2)-1 en +00
Donc j'ai étudie v=g-y en remarquant que (pi/2)=arctanx+arctan(1/x) en +00
Ainsi v(x)= xarctan(1/x)-1 d'où la nécessite de calculer la limite de xarctan(1/x)

L'approximation pour les petits angle est-elle utilisable de façon rigoureuse en mathématique?
On l'utilise en physique mais je ne sais pas si c'est recevable pour une démonstration comme celle ci.

[Carpate]

En posant :

[Pseuda]

L'approximation pour les petits angles ??

Dans ce cas (où tu n'as pas vu les équivalents ni les DL), tu peux utiliser le changement de variable :
arctan (1/x)=y, ssi 1/x = tan y et y appartient à ]-pi/2 , +pi/2[ ssi x = 1 / tan y.

Dès lors, lim x arctan (1/x) quand x->oo = lim y / tan y quand y-> 0 = 1 (car lim sin y / y = 1 en 0).

[Amoroth]

Merci à tous,
Oui tel que tan(x)=x pour les petits angles