Espace de Banach

[Bill BM]

Bonjour à tous!

S'il vous plait je veux des indications pour le problème suivant:

Notons l1 l’espace des suites complexes x = (xn)n;)N telles que ;)n;)0 |xn| < +;). On munit cet espace de la norme ||x|| = ;)n;)0 |xn| . Montrer que ( l1 , ||.|| ) est un espace de Banach

[mathelot]

Bjr,
||.|| est clairement une norme. Il reste à montrer que l1
est complet.

On note avec des lettres majuscules les points de l1. Ce sont donc des suites.



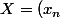Soit une suite de Cauchy (X_n) de l1. C'est une suite de suites.
Montrons qu'elle admet une limite.





l'indice du haut n'est pas un exposant mais un double indice.

Pour tout k fixé,
est une suite de Cauchy complexe, donc convergente vers

Mq que la suite (X_n) a pour limite la suite L=(l_k)

On considère une somme partielle finie de la série:



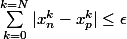
Quand n tend vers l'infini, on passe à la limite:



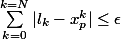
On passe à la limite sur N:




l1 est donc un Banach.

[Bill BM]

Merci bien

[mathelot]

La norme de l1 fait que , si deux suites X et Y sont "proches",
tous leurs termes de même indice sont "proches": x_n et y_n
et qu'en plus, les différences sont suffisamment petites
pour que la série , constituée des différences, soit sommable.