Dualite,orthogonalite

par **nemesis** » 07 Avr 2007, 19:17

bonsoir
soit U un sous ensemble de E* ;comment proceder pour montrer que

=

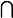
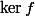
avec f

U

merci d'avance

par **serge75** » 07 Avr 2007, 19:33

Ne serait-ce pas plutôt l'orthogonale de U ?

par **serge75** » 07 Avr 2007, 19:36

x est dans m'orthogonale de U signifie que x est orthogonal à tous les f éléments de U, c'est à dire que pour tout f dans U on a f(x)=0, c'est à dire x est dans tous les Ker(f) pour f décrivant U. CQFD

par **nemesis** » 07 Avr 2007, 19:36

oui c'est ca

par **nemesis** » 07 Avr 2007, 19:40

ca m'enerve quand c'est aussi simple.......
merci encore

par **nemesis** » 07 Avr 2007, 19:41

donc on en deduit que l'orhogonale de U est formé de l'intersection de tous les noyaux de f appartenant à U ???

par **nemesis** » 07 Avr 2007, 19:54

Alors ,c'est bon pour dire ca ??

par **serge75** » 08 Avr 2007, 02:54

wep c'est ça ! c'étiat juste un jeu sur les définitions

Dualite,orthogonalite

Dualite,orthogonalite

Qui est en ligne