Bonjour,
Je fais de la topologie depuis peu en maths ( mi premier semestre ) et je ne comprends pas quelques choses:
Je ne comprends pas comment on "munit un espace d'une norme" et en quoi cette norme induit une distance.
( pour moi une distance et une norme c'est "à peu près la même chose" ), je ne comprends pas le fait qu'on utilise parfois la norme 1, la norme 2, la norme du sup... [ je suis assez perdu en topo ] quelqu'un pourrait m'expliquer ça par écrit? ( j'ai beau lire des cours, je bloque sur tout ça, espace métrique, vectoriel normé, etc..)
Souvent on doit montrer par exemple qu'un ensemble (E, ll.ll ) est de Banach mais je ne comprends pas comment par exemple.
Cordialement,
AlPeys.
Distance induite d'une norme.
9 messages
- Page 1 sur 1
Re: Distance induite d'une norme.
Salut,
Concernant la première question : Normes / Distances, ton cours contient forcément les axiomes définissant ce qu'est une "distance" sur un ensemble X absolument quelconque ainsi que les axiomes définissant ce qu'est un "norme" sur un espace vectoriel réel ou complexe.
Donc vu que tu as des définitions clairement différentes (et qu'en plus dans le cas des normes, la définition n'a de sens que dans le cadre d'un espace vectoriel), c'est évidement des trucs bien différents et c'est absolument pas "à peu prés la même chose".
Sauf que, lorsque tu as une norme ||.|| sur un e.v. E (donc un truc qui vérifie les axiomes d'une norme) et que tu considère (à tout à fait au hasard...) l'application qui à deux élément x et y de E associe le réel ||x-y||, ben tu constate que cette application vérifie effectivement les axiomes d'une "distance" donc ça permet de définir la notion de "distance induite par une norme" et en fait ça permet de dire qu'un espace vectoriel normé, ben c'est un cas particulier d'espace métrique mais il y a des tonnes d'espaces métriques qui ne sont pas des espaces vectoriels normés.
LE (gros) intérêt du bidule, c'est bien évidement que tout ce que tu va pouvoir définir/démontrer dans le cadre (général) des espaces métriques, ben ça sera en particulier vrai dans le cas es espaces vectoriels normés, mais le contraire est évidement faux.
Pour te donner une analogie (c'est même à mon sens plus qu'une analogie, c'est... la même chose) :
- Espace métriques = Mammifères.
- Espaces vectoriels normés = Rongeurs = "Sous catégorie" des Mammifères = "Cas particulier" de Mammifères.
Et évidement, tout ce qui est vrai pour l'ensemble des mammifères, ben c'est évidement vrai pour l'ensemble des rongeurs mais les rongeurs ont des spécificités qui ne sont pas valables pour l'ensemble des mammifères.
Concernant la première question : Normes / Distances, ton cours contient forcément les axiomes définissant ce qu'est une "distance" sur un ensemble X absolument quelconque ainsi que les axiomes définissant ce qu'est un "norme" sur un espace vectoriel réel ou complexe.
Donc vu que tu as des définitions clairement différentes (et qu'en plus dans le cas des normes, la définition n'a de sens que dans le cadre d'un espace vectoriel), c'est évidement des trucs bien différents et c'est absolument pas "à peu prés la même chose".
Sauf que, lorsque tu as une norme ||.|| sur un e.v. E (donc un truc qui vérifie les axiomes d'une norme) et que tu considère (à tout à fait au hasard...) l'application qui à deux élément x et y de E associe le réel ||x-y||, ben tu constate que cette application vérifie effectivement les axiomes d'une "distance" donc ça permet de définir la notion de "distance induite par une norme" et en fait ça permet de dire qu'un espace vectoriel normé, ben c'est un cas particulier d'espace métrique mais il y a des tonnes d'espaces métriques qui ne sont pas des espaces vectoriels normés.
LE (gros) intérêt du bidule, c'est bien évidement que tout ce que tu va pouvoir définir/démontrer dans le cadre (général) des espaces métriques, ben ça sera en particulier vrai dans le cas es espaces vectoriels normés, mais le contraire est évidement faux.
Pour te donner une analogie (c'est même à mon sens plus qu'une analogie, c'est... la même chose) :
- Espace métriques = Mammifères.
- Espaces vectoriels normés = Rongeurs = "Sous catégorie" des Mammifères = "Cas particulier" de Mammifères.
Et évidement, tout ce qui est vrai pour l'ensemble des mammifères, ben c'est évidement vrai pour l'ensemble des rongeurs mais les rongeurs ont des spécificités qui ne sont pas valables pour l'ensemble des mammifères.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Distance induite d'une norme.
Sinon, concernant le fait que l'on utilise plusieurs normes, ben déjà, ça vient du "gros théorème" (que vous risquez d'avoir admis) qui te dit que toutes les normes sur un même espace vectoriel de dimension finie sont équivalentes et qu'il s'ensuit que pour quasiment tout ce qu'on fait avec une norme (détermination des ensembles ouverts, fermés, bornés, calcul de limite de suites, de fonctions, etc, etc) la norme que l'on prend ne change rien au résultat.
Et évidement, ce fait là, il est génial vu qu'il signifie qu'à chaque fois qu'on veut montrer un truc, ben on peut choisir la norme qu'on veut et en particulier celle qui vont rendre les calculs les plus simples possibles.
Sinon, je comprend pas trop la dernière question : "je vois pas comment on montre que E est de Banach ?"
Ben... tu as une définition correspondant à "être de Banach" et tu regarde si c'est vrai ou pas pour l'espace E qu'on te donne.
Evidement en fonction du E donné, ça peut être plus ou moins simple/rapide, mais le principe c'est (forcément) toujours le même : une définition, ben c'est une définition...
Et évidement, ce fait là, il est génial vu qu'il signifie qu'à chaque fois qu'on veut montrer un truc, ben on peut choisir la norme qu'on veut et en particulier celle qui vont rendre les calculs les plus simples possibles.
Sinon, je comprend pas trop la dernière question : "je vois pas comment on montre que E est de Banach ?"
Ben... tu as une définition correspondant à "être de Banach" et tu regarde si c'est vrai ou pas pour l'espace E qu'on te donne.
Evidement en fonction du E donné, ça peut être plus ou moins simple/rapide, mais le principe c'est (forcément) toujours le même : une définition, ben c'est une définition...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Distance induite d'une norme.
Déjà, merci beaucoup pour ta réponse, j'y vois plus clair.
Soit c0 ={ (xn) ⊂ R: limn→∞ xn = 0 }
. On munit c0 de la norme ll(xn)ll∞ = sup |xn| avec n∈N
Montrer que (c0, ll·ll∞) est un espace de Banach.
En fait ce que je ne comprends pas, c'est " on munit l'espace d'une norme " cela veut dire que c0 représente un espace métrique?"
Et montrer qu'il est de Banach, c'est montrer qu'il est complet pour la distance associée à la norme.
Je ne parviens pas à le faire
Cordialement,
AlPeys. ( si possible simplement une indication, pas une réponse comportant le corrigé^^ )
Soit c0 ={ (xn) ⊂ R: limn→∞ xn = 0 }
. On munit c0 de la norme ll(xn)ll∞ = sup |xn| avec n∈N
Montrer que (c0, ll·ll∞) est un espace de Banach.
En fait ce que je ne comprends pas, c'est " on munit l'espace d'une norme " cela veut dire que c0 représente un espace métrique?"
Et montrer qu'il est de Banach, c'est montrer qu'il est complet pour la distance associée à la norme.
Je ne parviens pas à le faire
Cordialement,
AlPeys. ( si possible simplement une indication, pas une réponse comportant le corrigé^^ )
Re: Distance induite d'une norme.
Le "on munit l'espace de la norme", ben il veut dire.. ce que ça dit en général, c'est à dire qu'à partir de maintenant à chaque fois qu'on te parlera d'un truc qui se réfère à une norme, ça sera celle là, et qui si on te parle d'un truc qui se réfère à une distance alors ça sera la distance induite par cette norme là.
Sinon, au niveau "purement scolaire", ça te dit aussi qu'on te demande pas de vérifier que le bidule en question est effectivement une norme sur c0 (en fait ça signifie que tu l'a forcément déjà démontré dans un autre exercice et qu'on te fait grâce de recopier deux fois la même démonstration...)
Et, bis et répéta, ben ça te dit pas que "c0 représente un espace métrique", ça te dit que ll . ll∞est une norme sur l'espace vectoriel c0 (et on te fait aussi grâce de (re)démontrer que c0 est un espace vectoriel vu que tu l'a surement déjà fait).
Et "montrer qu'il est de Banach", ben faut évidement savoir quelle est la définition de "est de Banach" pour savoir ce qu'il faut démontrer (d'ailleurs, de façon générale, c'est pas con de savoir ce que signifie les mots qui sont employés dans les pharases qu'on lit).
Et en l'occurrence, "Être un espace de Banach", la définition, c'est "Être un espace vectoriel normé complet pour la distance issue de la norme".
Comme on te donne "gratos" le coté "être un espace vectoriel normé (i.e. on te demande pas de le (re)démontrer), il reste effectivement uniquement à démontrer que c0 mini de la distance induite par ll . ll∞ est complet.
Et concernant la façon de procéder, ben y'a pas trop le choix : tu prend une suite_{p\geq 0}) d'élément de c0 que tu suppose être de Cauchy (donc tu recopie évidement consciencieusement la définition de "être de Cauchy" pour voir ce que ça veut dire dans le contexte présent) et le but, c'est de montrer qu'elle est convergente vers un certain élément L de c0.
d'élément de c0 que tu suppose être de Cauchy (donc tu recopie évidement consciencieusement la définition de "être de Cauchy" pour voir ce que ça veut dire dans le contexte présent) et le but, c'est de montrer qu'elle est convergente vers un certain élément L de c0.
Bon, ben ensuite, forcément, il faut un peu se salir les mains : pour chaque p,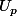 c'est un élément de c0 donc en fait c'est une suite :
c'est un élément de c0 donc en fait c'est une suite : _{n\geq 0}) et on a affaire à une suite... de suites...
et on a affaire à une suite... de suites...
De même, la limite L qu'on cherche, c'est un élément de c0 donc... une suite, c'est à dire le truc qu'on cherche, c'est un_{n\geq 0}) .
.
Tu as pas un début d'idée de ce que ça pourrait être ces fameux qu'on cherche ?
qu'on cherche ?
Reste évidement à prouver qu'ils existent puis que L est bien dans c0, puis que la suite (de suites)_{p\geq 0}) converge effectivement vers
converge effectivement vers  .
.
Sinon, au niveau "purement scolaire", ça te dit aussi qu'on te demande pas de vérifier que le bidule en question est effectivement une norme sur c0 (en fait ça signifie que tu l'a forcément déjà démontré dans un autre exercice et qu'on te fait grâce de recopier deux fois la même démonstration...)
Et, bis et répéta, ben ça te dit pas que "c0 représente un espace métrique", ça te dit que ll . ll∞est une norme sur l'espace vectoriel c0 (et on te fait aussi grâce de (re)démontrer que c0 est un espace vectoriel vu que tu l'a surement déjà fait).
Et "montrer qu'il est de Banach", ben faut évidement savoir quelle est la définition de "est de Banach" pour savoir ce qu'il faut démontrer (d'ailleurs, de façon générale, c'est pas con de savoir ce que signifie les mots qui sont employés dans les pharases qu'on lit).
Et en l'occurrence, "Être un espace de Banach", la définition, c'est "Être un espace vectoriel normé complet pour la distance issue de la norme".
Comme on te donne "gratos" le coté "être un espace vectoriel normé (i.e. on te demande pas de le (re)démontrer), il reste effectivement uniquement à démontrer que c0 mini de la distance induite par ll . ll∞ est complet.
Et concernant la façon de procéder, ben y'a pas trop le choix : tu prend une suite
Bon, ben ensuite, forcément, il faut un peu se salir les mains : pour chaque p,
De même, la limite L qu'on cherche, c'est un élément de c0 donc... une suite, c'est à dire le truc qu'on cherche, c'est un
Tu as pas un début d'idée de ce que ça pourrait être ces fameux
Reste évidement à prouver qu'ils existent puis que L est bien dans c0, puis que la suite (de suites)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Distance induite d'une norme.
( Encore merci ) pour la réponse, je n'ai pas le temps de chercher ce soir je vous mets ma réponse demain ( sur l'exercice que j'essaierai de résoudre! ) simplement la façon de procéder dont vous me parlez n'a pas été vue en cours ^^
Et merci quant à l'explication concernant le "on munit la norme"
Bien cordialement,
Alpeys.
Et merci quant à l'explication concernant le "on munit la norme"
Bien cordialement,
Alpeys.
Re: Distance induite d'une norme.
Je comprend de nouveau pas trop le sens de la phrase :Alpeys a écrit:...simplement la façon de procéder dont vous me parlez n'a pas été vue en cours...
- Si ce que tu sous-entend c'est que la notion de suite de Cauchy n'a pas été vue en cours, la, certes, ça crait un max vu que je vois pas comment on peut parler d'espace de Banach si on sait pas ce qu'est une suite de Cauchy.
- Si ce que tu sous-entend c'est que vous avez jamais fait la même preuve que celle là en cours, ben, perso, je trouverais plutôt çà bon signe : ça veut dire qu'on considère que vous êtes suffisamment grand pour être capable de faire autre chose que de simplement recopier mot à mot des trucs déjà faits...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Distance induite d'une norme.
Bonsoir,
alors comme promis j'ai essayé de résoudre le problème.
Il me paraît évident que toute suite de Cauchy de l'ensemble converge vers 0. Et 0 est dans l'ensemble.
Pour le montrer,
pour tout a > 0 , il existe N0 tq pour tout n > N0 on a:
d(xn,0) < a/2
Ensuite on applique la définition de Cauchy: pour tout m,p tels que:
m,p > N1 > N0, d(xm,xp) < d(xm,0)+d(0,xn) < a.
Ainsi pour n assez grand les suites xn convergent ( sont de cauchy ) vers l=0 qui appartient à l'ensemble ( ma démonstration me paraît bancale ).
Mais je n'arrive pas à utiliser le sup, toujours un problème avec " pour la distance issue de la norme ", je ne parviens pas à l'utiliser,
cordialement,
Alpeys.
alors comme promis j'ai essayé de résoudre le problème.
Il me paraît évident que toute suite de Cauchy de l'ensemble converge vers 0. Et 0 est dans l'ensemble.
Pour le montrer,
pour tout a > 0 , il existe N0 tq pour tout n > N0 on a:
d(xn,0) < a/2
Ensuite on applique la définition de Cauchy: pour tout m,p tels que:
m,p > N1 > N0, d(xm,xp) < d(xm,0)+d(0,xn) < a.
Ainsi pour n assez grand les suites xn convergent ( sont de cauchy ) vers l=0 qui appartient à l'ensemble ( ma démonstration me paraît bancale ).
Mais je n'arrive pas à utiliser le sup, toujours un problème avec " pour la distance issue de la norme ", je ne parviens pas à l'utiliser,
cordialement,
Alpeys.
Re: Distance induite d'une norme.
Bonsoir,
Beaucoup de choses sont à reprendre dans la démonstration
Je pense que la suite constante des _{n\in\N^*}) (suite de suites) est de Cauchy (essentiellement car elle est convergente), à valeurs dans
(suite de suites) est de Cauchy (essentiellement car elle est convergente), à valeurs dans  mais ne converge pas vers
mais ne converge pas vers  .
.
Qu'est-ce que ? Si c'est le terme général d'une suite de
? Si c'est le terme général d'une suite de  , alors c'est vrai, mais ça ne t'aidera pas trop (du moins pas dans ce que tu fais après). Si c'est le terme général d'une suite de suites, alors tu viens d'écrire exactement ce que tu voulais démontrer...
, alors c'est vrai, mais ça ne t'aidera pas trop (du moins pas dans ce que tu fais après). Si c'est le terme général d'une suite de suites, alors tu viens d'écrire exactement ce que tu voulais démontrer...
Pourquoi majorer) alors que tu veux une majoration de
alors que tu veux une majoration de ) ? (et au passage, il y a un p qui se transforme en n)
? (et au passage, il y a un p qui se transforme en n)
Bon, j'imagine que les sont des suites, mais on sait déjà qu'elles convergent vers 0 (donc qu'elles sont de Cauchy) par définition de
sont des suites, mais on sait déjà qu'elles convergent vers 0 (donc qu'elles sont de Cauchy) par définition de  .
.
Une piste pour aborder le problème
Il s'agit ici d'un problème de convergence uniforme de suites (pour reprendre les notations de Ben314, on veut montrer que quand
quand  ).
).
Pour ça, il faut déjà montrer que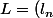_{n\in\N}) existe. Autrement dit, que, à
existe. Autrement dit, que, à  fixé,
fixé,  quand
quand  . En d'autres termes, c'est un problème de convergence simple.
. En d'autres termes, c'est un problème de convergence simple.
Puis il faut vérifier que la suite ainsi obtenue est bien dans
ainsi obtenue est bien dans  .
.
Bref, admettons qu'une telle suite existe. On veut montrer que pour tout
existe. On veut montrer que pour tout 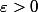 ,
,  pour
pour  assez grand. On est tenté d'utiliser l'inégalité triangulaire :
assez grand. On est tenté d'utiliser l'inégalité triangulaire :
 où
où  est à ajuster.
est à ajuster.
Là on se dit "le premier terme, on peut le majorer par en jouant sur
en jouant sur  puisque la suite est de Cauchy", mais le second... bah non puisqu'on veut justement montrer qu'il peut être aussi petit que l'on veut. Bref, on tourne en rond...
puisque la suite est de Cauchy", mais le second... bah non puisqu'on veut justement montrer qu'il peut être aussi petit que l'on veut. Bref, on tourne en rond...
Par contre si on réécrit l'inégalité triangulaire "sans les normes infinies" , à savoir sous la forme
 , où
, où  est fixé et
est fixé et  à ajuster, c'est différent (à toi de voir pourquoi )...
à ajuster, c'est différent (à toi de voir pourquoi )...
Beaucoup de choses sont à reprendre dans la démonstration
Il me paraît évident que toute suite de Cauchy de l'ensemble converge vers 0.
Je pense que la suite constante des
Pour le montrer,
pour tout a > 0 , il existe N0 tq pour tout n > N0 on a:
d(xn,0) < a/2
Qu'est-ce que
pour tout m,p tels que:
m,p > N1 > N0, d(xm,xp) < d(xm,0)+d(0,xn) < a.
Pourquoi majorer
Ainsi pour n assez grand les suites xn convergent ( sont de cauchy ) vers l=0
Bon, j'imagine que les
Une piste pour aborder le problème
Il s'agit ici d'un problème de convergence uniforme de suites (pour reprendre les notations de Ben314, on veut montrer que
Pour ça, il faut déjà montrer que
Puis il faut vérifier que la suite
Bref, admettons qu'une telle suite
Là on se dit "le premier terme, on peut le majorer par
Par contre si on réécrit l'inégalité triangulaire "sans les normes infinies" , à savoir sous la forme
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
