Comment peut on induire une distance depuis une norme ? Qu'est-ce que c'est une distance induite par une norme (je parle pas de l'explication par la formule d(x,y)=//×-y//mais plutôt au sens général )
Pourquoi doit on utiliser ces conditions pour montrer que c'est une distance induite par une norme ?
d(x,0)=//x//
d(¡x,¡y)=/i/d(x,y)
d(z+x,y+z)=d(x,y)
Distance induite par une norme
7 messages
- Page 1 sur 1
Re: Distance induire par une norme
Le sens général est donné par la formule
=\Vert y-x\Vert)
La distance de deux points, c'est la norme du vecteur ayant ces points pour origine et extrémité. C'est ça la distance induite par une norme ; que vas-tu chercher de plus ?
Je ne comprends pas ton autre question, d'autant plus que tu as visiblement fait une erreur dans ta dernière égalité. Tu voulais peut-être écrire=d(x,y)) ? Alors une distance qui vérifie ceci pour tous
? Alors une distance qui vérifie ceci pour tous 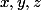 vérifie (en prenant
vérifie (en prenant 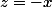 )
) =d(0,y-x)) . Et si
. Et si =\Vert y-x\Vert) ...
...
La distance de deux points, c'est la norme du vecteur ayant ces points pour origine et extrémité. C'est ça la distance induite par une norme ; que vas-tu chercher de plus ?
Je ne comprends pas ton autre question, d'autant plus que tu as visiblement fait une erreur dans ta dernière égalité. Tu voulais peut-être écrire
Re: Distance induire par une norme
Pour compléter un peu :
toute norme ||.. || induit une distance d(x,y) = || y - x ||
en revanche il existe des distance qui ne sont pas induite par une norme.
toute norme ||.. || induit une distance d(x,y) = || y - x ||
en revanche il existe des distance qui ne sont pas induite par une norme.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Distance induire par une norme
GaBuZoMeu a écrit:Le sens général est donné par la formule
La distance de deux points, c'est la norme du vecteur ayant ces points pour origine et extrémité. C'est ça la distance induite par une norme ; que vas-tu chercher de plus ?
Je ne comprends pas ton autre question, d'autant plus que tu as visiblement fait une erreur dans ta dernière égalité. Tu voulais peut-être écrire? Alors une distance qui vérifie ceci pour tous
vérifie (en prenant
)
. Et si
...
Je comprenais pas la différence entre 'toute norme est une distance ' et 'distance induite par une norme'
Pour la 2ème question oui c'était une erreur désolée je vais la corriger ,mais ce que cherche c'est plutôt une explication au sens théorique et général, par exemple les normes et leurs propriétés c'est des généralisations des vals absolus dans les mathématiques euclidiennes. Peut-être les conditions que j'ai déjà mentionné se sont les mêmes conditions pour définir un vecteur car comme tu as déjà dit' norme d'un vecteur ayant ces points pour origine et extrémité. '
J'espère que c'est un peut Claire pour toi
Re: Distance induite par une norme
Une norme c'est une fonction prenant pour argument un vecteur : cela en mesure la taille.
Une distance c'est une fonction prenant pour argument deux vecteurs : cela mesure la distance entre les deux extêmités.
Ce sont donc deux type de fonctions différentes.
En revanche si tu as une norme N, alors on peut construire une distance d(x,y) = N(y-x), ce qui veut dire que la distance entre les deux "points" x et y est la norme du vecteur allant de x à y.
Finalement, on peut construire des distances qui ne sont pas issues de normes.
Une distance c'est une fonction prenant pour argument deux vecteurs : cela mesure la distance entre les deux extêmités.
Ce sont donc deux type de fonctions différentes.
En revanche si tu as une norme N, alors on peut construire une distance d(x,y) = N(y-x), ce qui veut dire que la distance entre les deux "points" x et y est la norme du vecteur allant de x à y.
Finalement, on peut construire des distances qui ne sont pas issues de normes.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Distance induite par une norme
Une distance c'est une fonction prenant pour argument deux vecteurs
Je dirais plutôt deux éléments d'un ensemble : une distance n'est pas forcément définie sur un espace vectoriel. On peut par exemple définir une distance sur l'ensemble des mots de cinq lettres : la distance entre deux mots est définie comme le nombre d'emplacements où les deux mots ont des lettres différentes. Par exemple, la distance entre "cacao" et "carte" est 3. Exercice : vérifier qu'il s'agit bien d'une distance.
Re: Distance induite par une norme
Sylviel a écrit:Une norme c'est une fonction prenant pour argument un vecteur : cela en mesure la taille.
Une distance c'est une fonction prenant pour argument deux vecteurs : cela mesure la distance entre les deux extêmités.
Ce sont donc deux type de fonctions différentes.
En revanche si tu as une norme N, alors on peut construire une distance d(x,y) = N(y-x), ce qui veut dire que la distance entre les deux "points" x et y est la norme du vecteur allant de x à y.
Finalement, on peut construire des distances qui ne sont pas issues de normes.
Merci pour ta réponse j'y vois plus clair.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
