Bonjour,
Je dois calculer le développement limité à l'ordre 9 en 0 de tan(x), je sais qu'il n'a pas une formule à l'ordre n et je pourrais donc le calculer avec cos(x)/sin(x) mais à cette ordre ça serait très long et mon professeur à indiquer qu'il faut être "astucieux" , vous auriez une idée ?
Développement Limité
9 messages
- Page 1 sur 1
Re: Développement Limité
Avec cos(x)/sin(x), tu es mal parti. Je te conseille plutôt sin(x)/cos(x).
Par ailleurs la fonction tangente est impaire. Ça dit déjà des choses sur son d.l. en 0.
Par ailleurs la fonction tangente est impaire. Ça dit déjà des choses sur son d.l. en 0.
Re: Développement Limité
Salut,
\!=\!\sum_{n\geq 1}|B_{2n}|\dfrac{2^{2n}(2^{2n}\!-\!1)}{(2n)!}x^{2n-1})
Où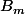 désigne le
désigne le  -ième Nombre de Bernoulli (suite de nombres "classique" qui apparait dans plusieurs domaines des mathématiques)
-ième Nombre de Bernoulli (suite de nombres "classique" qui apparait dans plusieurs domaines des mathématiques)
Sinon, concernant cette partie là de ta prose, c'est comme toujours plus ou moins exact de dire qu'il n'y a "pas de formule". Ce qui est exact, c'est qu'on ne peut pas exprimer le n-ième coefficient avec les symboles "usuels" des mathématiques, mais si on accepte des symboles moins "usuels", on peut écrire queArthurodur a écrit:. . . je sais qu'il n'a pas une formule à l'ordre n . . .
Où
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Développement Limité
Etre astucieux aujourd'hui c'est savoir utiliser le net , donc pourquoi pas la formule générale .
Les seules astuces auxquelles je pense sont
la division suivant les puissances croissantes , ou utiliser le dl de l'arctan .
Les seules astuces auxquelles je pense sont
la division suivant les puissances croissantes , ou utiliser le dl de l'arctan .
Re: Développement Limité
ma derniére réponse ( tan'=1+tan^2) donne un résultat rapide et facile à calculer .
Re: Développement Limité
tournesol a écrit:ma derniére réponse ( tan'=1+tan^2) donne un résultat rapide et facile à calculer .
soient les coefficients inconnus a,b,c,d réels
d'où le système
remarque
Re: Développement Limité
Très bonne méthode de mathelot et tournesol.
Une méthode similaire serait de poser des coefficients inconnus, et de les calculer en utilisant que tan et arctan sont bijections réciproques, et que le DL de arctan est connu (en primitivant le DL de 1/(1+x^2)
Une méthode similaire serait de poser des coefficients inconnus, et de les calculer en utilisant que tan et arctan sont bijections réciproques, et que le DL de arctan est connu (en primitivant le DL de 1/(1+x^2)
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
