Développement limité et puissance

[nix64]

Bonjours
pour calculer une puissance d un développement limité comme dans ce cas par exemple
on a

par contre à partir de la puissance 3 ça commence comme ici je peux aussi voire que
la c est un peu moins claire c est par par intuition que je vois

pour les puissances 4 et 5 et 6 je reste dans l intuition je me dit
et
et

d' abord est ce que j ai écrit est il correcte
et c est quoi la règle ou le truc qui me fait sortir de l intuition vers la lumière de l ampoule qui allume dans la tête et je me dit voila pour cette puissance de ce développement limité je m arrete a cet ordre là car pour le reste ça va t être un petit o

[mathelot]

bonsoir,
tu peux utiliser la formule du multinôme et ne garder que les termes de puissance inférieure ou égale à 6.

https://fr.wikipedia.org/wiki/Formule_du_multin%C3%B4me_de_Newton

[Mimosa]

Bonjour

Laisse tomber l'intuition et écris sérieusement les calculs, en ne négligeant que les termes de puissance supérieure à celle du .

Dès la première formule tu as au moins une erreur: dans le carré du premier membre il y a aussi qui est de degré 6, donc doit être gardé.

[nix64]

je suis sur qu il ya plus simple que cette formule de monôme j ai vue des truc que je ne comprends pas d ailleur des gens que regarde le monôme de plus bas degré dans le développementale et aussi d autre qui calcule avec facilité une puissance d un développement limité comme si ils savent déjà a quel ordre s arrêter exactement

[nix64]

Bonjour

Laisse tomber l'intuition et écris sérieusement les calculs, en ne négligeant que les termes de puissance supérieure à celle du .

Dès la première formule tu as au moins une erreur: dans le carré du premier membre il y a aussi qui est de degré 6, donc doit être gardé.

j ai rectifié maintenant c est juste mais il ya une methode pour simplifié les calculs

[nix64]

je crois que j ai trouvé la regle quelqun peut me le verifié ou me le contre dire
si m< ou = à m
si non

[nix64]

Bonjour

Laisse tomber l'intuition et écris sérieusement les calculs, en ne négligeant que les termes de puissance supérieure à celle du .

Dès la première formule tu as au moins une erreur: dans le carré du premier membre il y a aussi qui est de degré 6, donc doit être gardé.

on est pas obligé de faire tout le calcule
voila la formule pour calculé une puissance d un developpement limité d uen fonction


donc on doit calculé la puissance du polynome jusqu au monome de degré (n+1) -m c est a dire le developpement limité jusqu a l ordre n+1 - m

[aviateur]

Bonjour
qu'est ce que ça veut dire découvert et confirmé par moi?
D'autant plus que c'est faux!

[nix64]

Bonjour
qu'est ce que ça veut dire découvert et confirmé par moi?
D'autant plus que c'est faux!

maintenant c est pas faux

[pascal16]

Dès le départ, comme le terme constant est nul, on gagne un degré et on fini en o(x⁷).
Il faut bien développer tous les termes jusqu'à x⁶ et bien mettre o(x⁷).
Le DL ne change pas vu les 'trous' dans les puissances

Pour les cubes, o(x⁶) sera facteur d'au moins x², donc on va être en o(x⁸) et cette fois, on récupère bien un terme en x⁷

Les règles "générales" sont très améliorables.

PS : si vous ne voyez pas les caractères de puissance en unicode, dites-le.

[nix64]

PS : si vous ne votez pas les caractères de puissance en unicode, dites-le.

je n ai pas pas compris votez quoi ??!

[aviateur]

Bonjour
qu'est ce que ça veut dire découvert et confirmé par moi?
D'autant plus que c'est faux!

maintenant c est pas faux

Bonjour
Si c'est toujours aussi faux. Franchement ne cherche pas à balancer des résultats au pif. C'est pas comme ça qu'on fait des maths.
Prend un exemple simple, applique ce que quelqu'un t'a dit au dessus (je ne sais plus qui)
c'est à dire que tu développes ton expression en gardant que les termes d'ordre <= à n et tu verras que "ta formule" est archi-fausse.

[nix64]

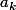
attention les coeficients peuvent etre nuls et meme nul on les prends on doit pas oublié leurs rang je ferai un exemple avec la formule et tu verra que c est vrai

[aviateur]

Bon tu insistes grossièrement alors j'abandonne!!

[nix64]

j ai pas volu etre grossier mais j ai utilisé cette formule pour trouver le developpement limité de la fonction reciproque de 2tanx - x et ça été juste c est pas que j insiste mais s il vous plait donne moi un contre exemple

[aviateur]

Je prend ce simple exemple: m=2 et n=1.
(1+x+o(x))^2 d'après toi ça fait 1^2+o(x)=1+o(x).

Mais (je mets les détails complets)
(1+x+o(x))^2=1+2x+2 o(x)+x^2 + 2 x o(x) +o(x)^2
c'est à dire (1+x+o(x))^2=1+2x+ o(x)

Je te conseille avant de chercher une formule éventuelle (une sorte de généralisation qui d'ailleurs n'a pas lieu à mon avis) de faire les calculs à la main.
Tous les exemples que tu as donné sont exactement comme celui que je viens de faire sauf que dans la pratique on n'écrit pas les termes dont on sait par avance qu'ils sont des o(x^n) (c'est à dire ici on ne mets pas ce qui en rouge.
Concernant ton exemple qui est surement intéressant tu pourrais le donner explicitement on pourra toujours de dire comment le traiter.

[mathelot]

autre exemple:






soit la formule du multinôme (de Newton)






d'où

[aviateur]

Evidemment de tout façon si tu développes tu as surement (sauf exception) des termes de x^j, j allant de 0 à n non nuls. Par quel magie vont-ils disparaitre.?
Attention @mathelot tu feras attention de ne pas oublier le dans l'écriture de cos(x). Je suppose que c'est un lapsus mais je dis ça pour les néophites.
Perso je ne ferai pas comme toi, car on peut faire ça à la main (même sans connaitre l'identité remarquable (a+b+...)^3, j'utilise (a+b+...)^2=somme de carrés + les doubles produits, c'est pas plus long et ça parait plus simple.)



puis on développe

[nix64]

@aviateur vous avez raison pour m>n c est faux
mais pour m< ou egal a n ça reste vrai la formule
je ne suis pas etrain d insister mais ça m as permis de beaucoup économiser le calcul
regarder avec moi pour m <= n s il vous plait

[nix64]

je vais ecrire l exemple que j ai cité c est un peux long