Bonjour,
Pourrais je avoir une explication pour le développement limité de 1/Cos à l'ordre 5 en 0.
Pour ma part, jai utilise le développement limité de cos puis de 1/1-u.
Cependant, pour 1/1-u, j'ai utilisé l'ordre 3. Mais je vois que l'ordre 2 suffit, ET je ne comprends pas cela !!
Mon problème vient du petit o.
Je veux un o(x^5) à la fin.
Mais j'ai un o(u^2) qui pour moi n'est pas égal à o(x^5)...
Merci d'avance!!!
Développement limité 1/cos(x)
6 messages
- Page 1 sur 1
Re: Développement limité 1/cos(x)
Merci pour ta réponse.
Je voulais utiliser 1/1-u,
Ça n'est pas possible?
Je voulais utiliser 1/1-u,
Ça n'est pas possible?
Re: Développement limité 1/cos(x)
Je voulais mettre la photo mais ça ne marche pas.
Dans mon livre, on part de 1/cos(x), puis on prend u = (x^2/2 - x^4/24 + o(x^5)) pis on a
1/ 1-u = ....
Mais je n'arrive pas à terminée car j'ai un o(u^2) qui pour moi n'est pas égal à o(x^5)
Dans mon livre, on part de 1/cos(x), puis on prend u = (x^2/2 - x^4/24 + o(x^5)) pis on a
1/ 1-u = ....
Mais je n'arrive pas à terminée car j'ai un o(u^2) qui pour moi n'est pas égal à o(x^5)
Re: Développement limité 1/cos(x)
Bonjour ;
Je prends le développement de cos(x) à l'ordre 5 : pour me distinguer de la proposition de chan79 .
 = 1 - \dfrac{x^2}{2} + \dfrac{x^4}{24} + o(x^5)) ,
,
donc :} = \dfrac{1}{1 -( \dfrac{x^2}{2} - \dfrac{x^4}{24} )+ o(x^5)} = 1 +( \dfrac{x^2}{2} - \dfrac{x^4}{24} )+( \dfrac{x^2}{2} - \dfrac{x^4}{24} )^2 + o(x^5))
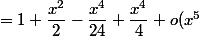 = 1 +\dfrac{x^2}{2} + \dfrac{5x^4}{24} +o(x^5) .)
Je prends le développement de cos(x) à l'ordre 5 : pour me distinguer de la proposition de chan79 .
donc :
Re: Développement limité 1/cos(x)
Merci pour votre réponse ! En fait c'était le o(x^5) qui me posait problème mais maintenant c'est bon 
Merci beaucoup !
Merci beaucoup !
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
