Bonjour à tous,
Je viens a peine de commencer les développements limités, et grâce à ma chance (ou pas), j'ai eu un exercice tout de suite en colle.
Mais je sèche déjà un peu.
Soit f définie par :
(sin sqrt(x)) / sqrt(x) si x>0
(sh sqrt(-x)) / sqrt(-x) si x<0
1 si x=0
Montrer que f est de classe C1. Est elle de classe C2 ?
Donc pour la première démonstration, il est évident que f est continue et dérivable sur \{0}. Je dois donc étudier le cas en 0.
Pour cela, j'exprime le taux de variation pour x>0 et pour x<0, et je fais ensuite x0 pour avoir la dérivée.
Donc pour x>0 j'ai (sin(sqrt(x))-(sqrt(x))/(x*sqrt(x)). La limite est une forme indéterminée, et la seule solution et de passer par le développement limité.
Mais comment fait on ?? Je connais le développement limité de la fonction sinus et racine, mais je ne sais pas comment les composer ?
J'ai pensé a faire le developpement limité de sin x a l'ordre 3 et d'ensuite remplacer x par sqrt(x), mais est ce correct ?
Merci à tous pour votre aide
Developpement limité et classe de fonction.
13 messages
- Page 1 sur 1
par girdav » 08 Juin 2010, 19:36
Bonjour,
oui, on peut poser
: ce qui fait que ça marche est que 
tend vers 
lorsque 
tend vers .
Tu peux faire le développement limité avec comme variable, ça simplifiera les écritures.
oui, on peut poser
Tu peux faire le développement limité avec
par lilano » 08 Juin 2010, 19:41
Ok merci pour la petite précision:
Je trouve donc
sinX = X - X^3/6 + o(X^3)
En soustrayant X puis en divisant par x*X, je retrouve la formule (sinX - X)/ x*X et qui tend vers 1/6.
Je fais de meme avec Sh X, et je devrais tomber sur la meme limite.
Merci beaucoup pour le petit coup de pouce =)
Pour ce qui est de la classe C2, je dois dériver les deux formules, puis recommencer un DL pour voir ce que ca donne ?
Je trouve donc
sinX = X - X^3/6 + o(X^3)
En soustrayant X puis en divisant par x*X, je retrouve la formule (sinX - X)/ x*X et qui tend vers 1/6.
Je fais de meme avec Sh X, et je devrais tomber sur la meme limite.
Merci beaucoup pour le petit coup de pouce =)
Pour ce qui est de la classe C2, je dois dériver les deux formules, puis recommencer un DL pour voir ce que ca donne ?
par girdav » 08 Juin 2010, 19:47
Je ne vois pas de solution plus simple. Avant de se lancer dans la dérivée une remarque (à laquelle tu as dû penser) est de "couper la fraction en deux" pour calculer plus facilement la dérivée.
par lilano » 08 Juin 2010, 19:58
Oui, c'est ce que je pensais faire, car la dérivée est un sacré morceau tout de même (mais déjà plus l'habitude que les développements limités)
L'equivalence sin x ~ x nous ramène a une forme indeterminée puisque l'on aura 0 au numérateur et 0 au dénominateur non ?
L'equivalence sin x ~ x nous ramène a une forme indeterminée puisque l'on aura 0 au numérateur et 0 au dénominateur non ?
par busard_des_roseaux » 08 Juin 2010, 20:12
lilano a écrit:Pour ce qui est de la classe C2, je dois dériver les deux formules, puis recommencer un DL pour voir ce que ca donne ?
c'est bizarroïde ton truc .. un DL ne donne même pas la dérivabilité.
exemple:
par lilano » 08 Juin 2010, 20:22
Eh bien pour x>0
f'(x)= (X*cos X - sin X) / 2*x*X
Si x --> 0 alors X*cosX - sin X --> 0 ainsi que 2*x*X donc on a une forme indéterminée.
L'equivalence de sin x ~ x n'est pas d'une tres grande aide ici non ?
C'est pourquoi je pense qu'il faut faire un développement limité, je ne vois pas d'autre solution en fait...
f'(x)= (X*cos X - sin X) / 2*x*X
Si x --> 0 alors X*cosX - sin X --> 0 ainsi que 2*x*X donc on a une forme indéterminée.
L'equivalence de sin x ~ x n'est pas d'une tres grande aide ici non ?
C'est pourquoi je pense qu'il faut faire un développement limité, je ne vois pas d'autre solution en fait...
par Doraki » 08 Juin 2010, 21:36
lilano a écrit:Donc pour x>0 j'ai (sin(sqrt(x))-(sqrt(x))/(x*sqrt(x)). La limite est une forme indéterminée, et la seule solution et de passer par le développement limité.
Mais comment fait on ?? Je connais le développement limité de la fonction sinus et racine, mais je ne sais pas comment les composer ?
Le développement limité de racine carrée n'est pas un "vrai" développement limité. (déjà c'est même pas dérivable en 0).
Donc c'est assez risqué de parler de composer le DL de sinus avec un hypothétique DL de racine carrée.
En revanche, on a le droit de composer par une fonction continue dans une limite :
Si
Ce qui devrait débloquer le calcul des dérivées.
par busard_des_roseaux » 09 Juin 2010, 07:25
Bj,
tout à fait d'accord avec Doraki ! on peut remplacer x par
dans un DL pour calculer une limite, mais sans écrire que l'on compose des DL car
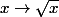n'est pas un DL de 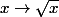puisque ce n'est pas une fonction polynôme
on a donc, pour x de signe quelconque
 \over x}=1 - {x^2 \over 6}+o(x^2))
 \over x}=1 + {x^2 \over 6}+o(x^2))
d'où
 \over \sqrt{x}}=1 - {x \over 6}+o(x))
 \over \sqrt{-x}}=1 - {x \over 6}+o(x))
d'où
f se prolonge en x=0 par f(0)=1
f est dérivable en x=0 et= {-1 \over 6})
Avec la formule de dérivation de Leibniz, on calcule f'(x) pour x>0
={\sqrt{x} cos(\sqrt{x}) - sin(\sqrt{x}) \over 2 \sqrt{x}})
={- x \sqrt{x} \over 6 x\sqrt{x}}+{x \over 60} +o(x))
={- 1 \over 6 }+{x \over 60} +o(x))
d'où la continuité de f ' à droite en x=0
d'où
={1 \over 60})
.
A gauche, on calcule f'(x) pour x0 et x<0
écrire des DL généralisés. vérifier que f'' n'est pas continue :mur:
tout à fait d'accord avec Doraki ! on peut remplacer x par
dans un DL pour calculer une limite, mais sans écrire que l'on compose des DL car
on a donc, pour x de signe quelconque
d'où
d'où
f se prolonge en x=0 par f(0)=1
f est dérivable en x=0 et
Avec la formule de dérivation de Leibniz, on calcule f'(x) pour x>0
d'où la continuité de f ' à droite en x=0
d'où
A gauche, on calcule f'(x) pour x0 et x<0
écrire des DL généralisés. vérifier que f'' n'est pas continue :mur:
par lilano » 13 Juin 2010, 17:10
Merci beaucoup pour votre aide.
J'ai eu l'exercice alors que je n'avais pas vu encore le changement d'echelle des DL, donc je comprends mieux pourquoi on peut mettre la racine dans le sinus.
Mais donc pour montrer que la fonction ou la dérivée est continue, le DL pour x>0 et x<0 suffit donc ?
J'ai eu l'exercice alors que je n'avais pas vu encore le changement d'echelle des DL, donc je comprends mieux pourquoi on peut mettre la racine dans le sinus.
Mais donc pour montrer que la fonction ou la dérivée est continue, le DL pour x>0 et x<0 suffit donc ?
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :