Dérivées et intégrales de fonctions bijectives

[hcl]

Bonjour,

je cherche des infos sur des fonctions bijectives particulières (x=f(t)) dont les dérivées de tous ordre (dx/dt, d2x/dt2, ...) et les intégrales de tous ordres (/xdt, //(xdt)dt, ...)seraient aussi des bijections.
De telles fonctions existent-elles, en dehors des droites, et si oui auriez-vous un exemple ou même simplement des informations à leur propos ?

Merci pour votre aide.
Cordialement
Hervé

[Chimomo]

Bien sur que de telles fonction existent en dehors des droites. D'ailleurs si une fonction est de classe Ck et bijective et que sa réciproque est de classe Ck on dit que cette fonction est un Ck difféomorphisme. Les Cinfini difféomorphisme sont donc des fonctions qui remplissent tes conditions.

On montre que si une fonction est Ck et bijective et que sa dérivée ne s'annule pas alors c'est un Ck difféomorphisme.

[El_Gato]

Si tu t'intéresses uniquement aux difféomorphismes alors la structure de cet ensemble de fonctions est connue: ce sont toutes les bijections strictement monotones et indéfiniment différentiables, dont les dérivées de tout ordre sont strictement monotones et différentiables.

Par contre la structure de l'ensemble des difféomorphismes , avec 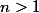est énormément plus complexe.

[hcl]

Hello,
Merci beaucoup pour votre aide. je suis hélas assez peu mathématicien et je ne connais rien à ces difféomorphismes. Ces fonctions m'intéressent dans le cadre d'un travail en physique théorique. Auriez-vous des liens vers des sites qui m'en diraient plus, et éventuellement (oui je rêve :lol3:) qui donneraient des exemples pratiques ?

A vous lire, avec tous mes remerciements,
Cordialement
Hervé

[El_Gato]

1- Une remarque au passage: une "droite", c'est à dire une fonction affine, n'est pas un exemple de fonction dont tu as écris les propriétés: la dérivée première n'est pas une bijection dans ce cas. Les avec 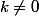sont parmi les exemples les plus simples de fonctions satisfaisant aux propriétés requises.

2- Les difféomorphismes, qu'ils soient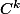 , ou analytiques () sont très utilisés en physique théorique. Car, basiquement, la physique théorique c'est surtout des maths, et pas des faciles.

3- Ceci étant dit, le cas des difféomorphismes en dimension 1 (c'est à dire des difféos ) relève d'un théorème basique de topologie en dimension 1, donné dans tous les cours d'analyse, et qui élucide la structure de l'ensemble des homéomorphismes en dimension 1. Voir par exemple Dieudonné, Eléments d'Analyse, tome 1, chapitre IV. Cela n'empêche pas l'apparition de dynamiques très compliquées même en dimension 1, mais on a au moins un théorème fort dans ce cas là.

4- Pour comprendre la difficulté du problème en dimension supérieure, il suffit de noter qu'une classe importante de difféomorphismes s'obtient en prenant le flot d'un champ de vecteurs de classe . En dimension 1, entre deux points singuliers, c'est à dire entre deux zéros du champ, on a un homéomorphisme différentiable strictement monotone. Donc c'est "assez simple" dans ce cas. Or, rien qu'en dimension 2, imaginer toutes les formes d'orbites qu'on peut obtenir à partir des champs de vecteurs... (voir par exemple: "Systèmes différentiels, étude graphique" par V. Gautheron chez F. Nathan). De plus, en dimension 2, les singularités ont la liberté d'apparaitre dans un continuum bidimensionnel, dans lequel il n'y a plus de structure d'ordre canonique lié à la topologie.

Mais, d'après ton post initial, tu ne sembles intéressé que par la dimension 1, cas pour lequel on dispose du théorème générique rappelé ci-dessus.

[hcl]

Super, merci ! Je commence à comprendre certaines choses, qui collent d'ailleurs bien à ce que je commençais à entrevoir, mais j'ai un peu de mal avec la terminologie à laquelle je ne suis pas habitué.

Dois-je comprendre qu'un difféomorphisme de classe Ck sera une bijection jusqu'à la kième dérivée, ou intégrale, tandis que la classe Cinfini concernera des dérivations à l'infini (type exp(x)) ?

Cordialement
Hervé

[El_Gato]

Un difféomorphisme est une application ( ouvert de ) telle que:

1- est une bijection de sur .
2- , ainsi que 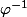sont toutes deux différentiables.

Une application est de classe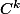 si ses dérivées jusqu'à l'ordre k sont continues. De classe si les dérivées de n'importe quel ordre sont continues.

Si un difféomorphisme est de classe 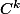(resp. ) alors 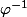l'est aussi et on parle alors de 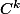(resp. )-difféomorphisme.

Physiquement, un difféomorphisme, lorsqu'il provient du flot d'un champ de vecteurs (ou plus généralement d'une "difféotopie"), est associé aux phénomènes "lisses", réversibles, et dont la réversion est également "lisse".

Cela dit, les fonctions qui t'intéressent doivent satisfaire des propriétés encore plus fortes, puisque tu demandes en plus que certaines intégrales multiples associées à tes fonctions soient bijectives.

[hcl]

Grand merci pour tout cela.
A vrai dire ce qui m'intéresse essentiellement ce sont les fonctions qui sont bijectives et dont la dérivée première ainsi que l'intégrale première sont aussi des bijections. Je n'ai pas vraiment besoin d'utiliser d'ordres supérieurs, mais je me renseigne au cas où.

Il m'apparaît, peut-être à tort, qu'une trajectoire x=f(t), continue et dérivable, peut toujours être découpée en segments dans lesquels l'intégrale de la trajectoire ainsi que sa dérivée sont des bijections. Typiquement de tels segments seraient compris entre un point d'inflexion de la trajectoire et un extremum de celle-ci. Hélas je ne sais pas démontrer que cette propriété existe. Crois-tu qu'une telle démonstration est possible ?

A te lire
Cordialement
Hervé

[mathelot]

Il m'apparaît, peut-être à tort, qu'une trajectoire x=f(t), continue et dérivable, peut toujours être découpée en segments dans lesquels l'intégrale de la trajectoire ainsi que sa dérivée sont des bijections.

je signale le contre exemple et qui est de classe et pour laquelle la découpe en intervalles n'est pas de cardinal fini.

cordialement.

[El_Gato]

je signale le contre exemple et qui est de classe et pour laquelle la découpe en intervalles n'est pas de cardinal fini.

cordialement.

Oui, mais hcl n'a pas imposé une découpe en un nombre fini de tels segments.

Dans le cas de la fonction f que tu cites, on peut bien découper le domaine de f privé de 0 en intervalles (dont les longeurs deviennent de plus en petites à mesure que l'on s'approche de 0) tels que, sur chaque segment, f soit un difféomorphisme.

La difficulté en 0 provient du fait que 0 n'est pas un extrêmum isolé de la dérivée.

On doit probablement pouvoir construire à partir de ta fonction f des exemples encore plus pathologiques où le phénomène observé en 0 s'étend par densité à un ensemble dense dénombrable sur la droite, par exemple en considérant pour une énumération des rationnels.

Cela dit, je crois que, dans un contexte physique, qui est celui qui intéresse hcl, on doit pouvoir supposer raisonnablement qu'on se place en dehors de ces cas pathologiques, et que x = f(t) peut effectivement être découpé en intervalles sur lesquels c'est strictement monotone. Cela n'est pas vrai mathématiquement au sens le plus général, mais l'est sûrement lorsque l'on se restreint à des fonction x = f(t) plus régulières, les splines cubiques par exemple.

[hcl]

Cela dit, je crois que, dans un contexte physique, qui est celui qui intéresse hcl, on doit pouvoir supposer raisonnablement qu'on se place en dehors de ces cas pathologiques, et que x = f(t) peut effectivement être découpé en intervalles sur lesquels c'est strictement monotone. Cela n'est pas vrai mathématiquement au sens le plus général, mais l'est sûrement lorsque l'on se restreint à des fonction x = f(t) plus régulières, les splines cubiques par exemple.

Oui, absolument, c'est bien ce dont je parle.
Y aurait-il une façon de nommer de tels segments de trajectoires ? Pour le moment je les décrits comme des "segments bijectifs" mais j'ai bien conscience que cette terminologie est impropre.

A vous lire, avec encore tous mes remerciements pour l'aide que vous m'apportez,
Cordialement
Hervé