Derivee n-ieme de 1/u
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 13 Jan 2011, 18:39
par Anonyme » 13 Jan 2011, 18:39
Bonsoir,
Je cherche a trouver l'expression générale de la dérivée n-ieme de
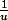
par rapport a x. J'ai pense a faire les 1ere dérivée a la main pour conjecturer puis faire une récurrence mais j'ai réussi a la main a calculer

et

mais j'ai pas pu conjecturer grand chose. A partir de la lexpression devient trop compliquer et je sais pas comment la faire calculer par wolfram.
Alors comment faire ?
Merci
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Jan 2011, 18:41
par girdav » 13 Jan 2011, 18:41
Bonsoir,
au fur et à mesure que l'on dérive la puissance au dénominateur augmente. On peut conjecturer que
}(x) =\fr{c_n}{x^{n+1}})
avec

à déterminer.
-
Anonyme
 par Anonyme » 13 Jan 2011, 18:50
par Anonyme » 13 Jan 2011, 18:50
Oui ça j'avais trouvé . J'ai trouve aussi que

comporte
}\time{u}^{n})
et
^n)
(le signe dépend de la parité)
Je pense qu'en calculant la dérivée 5eme je devrais avoir une idée plus précise de la forme des autres termes mais j'ai trop la flemme de la calculer. Est ce que quelqu'un peut le faire au moyen d'un logiciel de calcul formel ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Jan 2011, 18:51
par girdav » 13 Jan 2011, 18:51
Pas besoin de tout ça, on peut obtenir un lien de récurrence entre
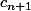
et

.
-
Anonyme
 par Anonyme » 13 Jan 2011, 18:55
par Anonyme » 13 Jan 2011, 18:55
Au fait c'est pas x au dénominateur mais u.
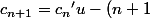u'\time{c_n})
mais ca ne m'avance pas trop.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Jan 2011, 18:59
par girdav » 13 Jan 2011, 18:59
Qmath a écrit:Au fait c'est pas x au dénominateur mais u.
J'avais noté

dans mon message mais ce n'est de toute façon pas le problème puisque l'on peut donner le nom que l'on veut tant que l'on reste cohérent.
Qmath a écrit: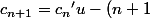u'\time{c_n})

est une constante.
-
Anonyme
 par Anonyme » 13 Jan 2011, 19:08
par Anonyme » 13 Jan 2011, 19:08
girdav a écrit:
est une constante.
Pourquoi ? c_n dépend de u et de ces dérivées qui dépendent de x ..
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Jan 2011, 19:10
par girdav » 13 Jan 2011, 19:10
Qmath a écrit:Je cherche a trouver l'expression générale de la dérivée n-ieme de
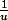
par rapport a x.
Je croyais que l'on cherchait tout bêtement la dérivée

-ième de

alors qu'en fait c'est la dérivée de
})
. En effet, c'est plus délicat.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 13 Jan 2011, 19:11
par Doraki » 13 Jan 2011, 19:11
comme le dit girdav depuis le début on peut conjecturer que cn ne dépend pas de x et est une fonction constante.
Si t'as calculé f', f'', f''', tu peux regarder les fonctions constantes c1,c2,c3 qui y correspondent.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Jan 2011, 19:16
par girdav » 13 Jan 2011, 19:16
Sinon, on a une formule générale pour la dérivée

-ième d'une composée, mais je ne me souviens plus du nom. On doit pouvoir la retrouver à la main mais elle n'est pas spécialement jolie (comme la formule que l'on cherche je suppose).
-
Anonyme
 par Anonyme » 13 Jan 2011, 19:17
par Anonyme » 13 Jan 2011, 19:17
Je me demande s'il n'est pas plus simple de chercher la formule générale de
^{(n)})
puis de chercher une formule de
^{(n)})
je pense que la forme de cette dernière doit être plus sympathique comparé a celle de
^{(n)})
.
Qu'en penses tu ?
Edit: grillé :marteau:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Jan 2011, 19:36
par Nightmare » 13 Jan 2011, 19:36
Pour vous encourager à vous décourager, lire [url="http://www.math.ens.fr/culturemath/maths/pdf/analyse/derivation.pdf"]ce poly[/url]
:happy3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Jan 2011, 19:38
par girdav » 13 Jan 2011, 19:38
C'est pile l'endroit où j'avais vu la formule et je comprends pourquoi je ne l'ai jamais sue.
-
Anonyme
 par Anonyme » 13 Jan 2011, 19:43
par Anonyme » 13 Jan 2011, 19:43
Ah ok il y a tout une théorie derrière et moi qui espérais trouver quelque chose avec mes petits calculs a la main :ptdr:
C'est a quel niveau qu'on voit cela ?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Jan 2011, 19:47
par benekire2 » 13 Jan 2011, 19:47
Ouais c'est pile poil l'endroit où j'avais vu le résultat également.
Qmath >> La dérivée n ième de x --> 1/x tu y arriveras sans trop de mal. fog un peu moins mais je crois qu'on peut faire plus simple que le pdf ...
EDIT. En fait , je connais que la formule de Faa di Bruno , celle du pdf ... :marteau:
-
Anonyme
 par Anonyme » 13 Jan 2011, 19:57
par Anonyme » 13 Jan 2011, 19:57
Pour 1/x c'est assez facile mais pour la formule de fog je pense que je devrais attendre quelques semaines histoire que les exams se terminent j'aurais besoin de beaucoup de temps. :lol3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Jan 2011, 20:12
par Nightmare » 13 Jan 2011, 20:12
Qmath a écrit:C'est a quel niveau qu'on voit cela ?
C'est assez curieux, j'ai remarqué depuis quelque temps, à quel point vous (quelques lycéens habitués du forum) associez quasiment systématiquement une notion mathématique à un niveau d'étude.
A partir du supérieur, ce qu'on enseigne selon les années est quand même très dépendant de l'école/fac dans laquelle on étudie (même si on pourrait parler d'un tronc global commun, et encore...). Et puis en dehors de ça, en tant que passionnés des maths que vous êtes, le niveau "scolaire" des notions ne devraient pas vous intéresser, par contre, le niveau "mathématique" nécessaire à la compréhension de la notion lui, est plus important ! Et vous conviendrez qu'il y a un grand gap entre les deux. Par exemple, la plupart des personnes qui étudient la théorie de Galois le font scolairement en bac+4/5, mais ce n'est pas pour autant qu'un élève qui sort de sup ne pourrait pas la comprendre...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Jan 2011, 20:20
par benekire2 » 13 Jan 2011, 20:20
On a été formaté comme ça :zen:
Non plus sincèrement j'essaie de me détacher de ces "étiquettes" mais c'est pas tout le temps facile ; et je pense que Qmath avait plus en tête l'idée de "est-ce que je vais y comprendre quelque chose si je lis des machins autour de cette théorie".
Souvent quand je fais une recherche et que je tombe sur un document qui sort d'une fac, je lis le début , si je comprends je continue , sinon j'arrête , je regarde pas trop "l'année qui correspond" même s'il y a une forte similitude entre le taux d'abandon de lecture et "l'année correspondante" ...
-
Anonyme
 par Anonyme » 13 Jan 2011, 20:24
par Anonyme » 13 Jan 2011, 20:24
Tu as parfaitement raison.
En posant cette question je ne m'attendais certainement pas a une réponse du type :" tu aborderas cette notion au début du 2eme semestre de la L2" mais plutôt "pour pouvoir l'aborder fraudait avoir un bagage de sup" qui renseigne comme tu l'a dis sur le niveau mathématiquement requis.
On est en accord sur le sujet c'est juste un abus de langage. Je devrais peut être demander qu'elle notions sont requises pour pouvoir aborder cette notion ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Jan 2011, 20:30
par Nightmare » 13 Jan 2011, 20:30
Dans ce cas, à la lecture du poly, tout les prérequis en théorie des graphes sont expliqués donc à priori la seule chose à savoir c'est ce qu'est une dérivée :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités