Bonjour,
Je cherche à déterminer le nombre façons de décomposer un K-espace vectoriel de dimension q en une somme directe de deux sous-espaces (K est de cardinal p). Quelqu'un pourrait-il m'aider ?
Merci
Dénombrement des décompositions en sommes directes
6 messages
- Page 1 sur 1
Re: Dénombrement des décompositions en sommes directes
Salut,
Si K est de cardinal et que E est un K e.v. de dimension
et que E est un K e.v. de dimension  alors pour fabriquer une base de E, il faut commencer par choisir un vecteur non nul, puis un vecteur non colinéaire au premier puis un vecteur non combinaison linéaire des deux premiers, etc...
alors pour fabriquer une base de E, il faut commencer par choisir un vecteur non nul, puis un vecteur non colinéaire au premier puis un vecteur non combinaison linéaire des deux premiers, etc...
Bref, le nombre de base de E c'est(p^q\!-\!p)(p^q\!-\!p^2)...(p^q\!-\!p^{q-1}))
Ensuite, si tu fixe un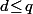 et que tu cherche le nombre
et que tu cherche le nombre 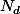 de façon d'écrire
de façon d'écrire 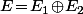 avec
avec \!=\!d) (donc forcément
(donc forcément \!=\!q\!-\!d) ) il suffit de compter de deux façons différentes le nombre de base de E.
) il suffit de compter de deux façons différentes le nombre de base de E.
- D'un coté, le nombre de base de E est évidement égal à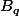 .
.
- D'un autre coté, pour choisir une base de E, on peut commencer par choisir une écriture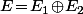 , puis une base
, puis une base 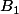 de
de  et une base
et une base 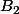 de
de  pour prendre au final la concaténation de
pour prendre au final la concaténation de 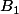 et
et 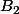 (toute base de E est obtenue de manière unique par ce procédé). Donc le nombre de base de E est aussi égal à
(toute base de E est obtenue de manière unique par ce procédé). Donc le nombre de base de E est aussi égal à 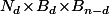
Bilan : (qui doit pas mal se simplifier avec des polynômes cyclotomiques mais j'ai pas regardé...)
(qui doit pas mal se simplifier avec des polynômes cyclotomiques mais j'ai pas regardé...)
Et sauf erreur, le truc que tu cherche c'est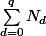 (si tu compte comme différentes les écritures
(si tu compte comme différentes les écritures 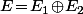 et
et 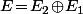 )
)
Si K est de cardinal
Bref, le nombre de base de E c'est
Ensuite, si tu fixe un
- D'un coté, le nombre de base de E est évidement égal à
- D'un autre coté, pour choisir une base de E, on peut commencer par choisir une écriture
Bilan :
Et sauf erreur, le truc que tu cherche c'est
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Dénombrement des décompositions en sommes directes
Merci bien !
Ne pensez-vous pas qu'on peut simplifier considérablement la solution avec des quotients de groupes ?
Ne pensez-vous pas qu'on peut simplifier considérablement la solution avec des quotients de groupes ?
Re: Dénombrement des décompositions en sommes directes
Salut,
Dans l'idée des quotients tu peux penser à ça :
Soit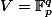 ton espace vectoriel et
ton espace vectoriel et 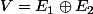 une décomposition en somme directe. Soit
une décomposition en somme directe. Soit 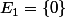 soit il contient une droite. Grâce à cette considération en notant
soit il contient une droite. Grâce à cette considération en notant 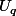 le nombre de décompositions que tu cherches tu as une formule récurrente pour
le nombre de décompositions que tu cherches tu as une formule récurrente pour 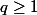 :
:
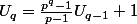
Avec la convention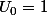 . Le
. Le 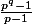 est le cardinal de
est le cardinal de ) , l'ensemble des droites de
, l'ensemble des droites de  et le
et le 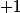 de la décomposition triviale
de la décomposition triviale 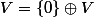 . Et lorsqu'on a une droite
. Et lorsqu'on a une droite  fixée l'ensemble des décompositions
fixée l'ensemble des décompositions 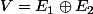 telles que
telles que 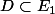 est en bijection avec celles de
est en bijection avec celles de 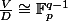 .
.
Est-ce à cela que tu pensais ?
On a une formule récurrente mais c'est pas sûr qu'on puisse la résoudre facilement par contre. La formule de Ben sera peut-être plus pratique à manipuler, à toi de voir.
À voir si ça marche, il est tard j'ai peut-être les neurones qui dysfonctionnent .
.
Bonne nuit.
Dans l'idée des quotients tu peux penser à ça :
Soit
Avec la convention
Est-ce à cela que tu pensais ?
On a une formule récurrente mais c'est pas sûr qu'on puisse la résoudre facilement par contre. La formule de Ben sera peut-être plus pratique à manipuler, à toi de voir.
À voir si ça marche, il est tard j'ai peut-être les neurones qui dysfonctionnent
Bonne nuit.
Re: Dénombrement des décompositions en sommes directes
Salut, de E (=>
de E (=>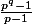 possibilité) puis que tu choisi une décomposition en somme directe F1+F2 de l'e.v. quotient F=E/
possibilité) puis que tu choisi une décomposition en somme directe F1+F2 de l'e.v. quotient F=E/ . Certes, en procédant de la sorte, tu as une décomposition, mais il y a plusieurs façon d'obtenir la même décomposition vu que partant de E=E1+E2, il y a plusieurs façons de choisir la droite vectorielle
. Certes, en procédant de la sorte, tu as une décomposition, mais il y a plusieurs façon d'obtenir la même décomposition vu que partant de E=E1+E2, il y a plusieurs façons de choisir la droite vectorielle  de E1.
de E1.
Il faut donc diviser ton truc par le nombre de façons de choisir dans E1 modulo de fixer d'avance la dimension de E1 pour que ce "nombre de façon" ne dépende pas de E1.
dans E1 modulo de fixer d'avance la dimension de E1 pour que ce "nombre de façon" ne dépende pas de E1.
Et au final, ben tu doit retomber super rapidement sur la même formule que moi au dessus (qui est très simple pour une dimension d de E1 fixée, mais sans doute pas très simple si on somme sur tout les d)
Sinon, en regardant comment ça se simplifie, j’obtiens que}\prod_{\delta}\Phi_\delta(p)) où
où ) est le
est le  -ième polynôme cyclotomique et où le produit s'effectue sur les
-ième polynôme cyclotomique et où le produit s'effectue sur les 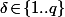 tels que le reste de la division de
tels que le reste de la division de  par
par  soit strictement inférieur au reste de la division de
soit strictement inférieur au reste de la division de  par
par  .
.
Pas sûr qu'on puisse exprimer plus simplement l'ensemble des sur lequel on fait le produit et encore moins sûr qu'on puisse sommer facilement les
sur lequel on fait le produit et encore moins sûr qu'on puisse sommer facilement les 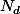 ...
...
Sauf erreur, ça déconne : là ton calcul correspond à dire que tu commence par choisir une droite vectorielleArchytas a écrit:...
Il faut donc diviser ton truc par le nombre de façons de choisir
Et au final, ben tu doit retomber super rapidement sur la même formule que moi au dessus (qui est très simple pour une dimension d de E1 fixée, mais sans doute pas très simple si on somme sur tout les d)
Sinon, en regardant comment ça se simplifie, j’obtiens que
Pas sûr qu'on puisse exprimer plus simplement l'ensemble des
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Dénombrement des décompositions en sommes directes
Bien vu ! J'avais pas fait gaffe à ce détail ^^.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
