Découpage d'un hypersandwich

par **Nightmare** » 12 Jan 2009, 23:58

Bonsoir :happy3:

Un exercice bien sympathique que je vous soumets, une belle application des maths à la vie courante :

On considère un sandwich au poulet. Montrer que l'on peut le découper d'un seul coup de couteau de telle sorte que les deux parties aient chacune autant de pain et de poulet que l'autre.

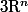
Généralisation à un hypersandwich : On se donne un hypersandwich () composé de n-1 hyperingrédients. Montrer que l'on peut découper l'hypersandwich avec un hypercouteau de telle sorte qu'il y ait la même quantité de chaque hyperingrédients dans les deux parties.

(Première mission, décrypter l'énoncé :lol3:)

A vous de jouer.

Edit Moi même : Il y a n-1 hyperingrédients et non n comme je l'avais écrit.

par **Joker62** » 13 Jan 2009, 00:16

Y'est 00h ! J'suis dans mon lit, J'me disais que j'avais faim et je vois ton post !
Merci d'avoir gâché ma nuit Jordan !

par **anima** » 13 Jan 2009, 00:23

Joker62 a écrit:Y'est 00h ! J'suis dans mon lit, J'me disais que j'avais faim et je vois ton post !
Merci d'avoir gâché ma nuit Jordan !

Tu peux surement t'amuser a faire une preuve empirique, et ainsi combler ta faim :we:

par **Doraki** » 13 Jan 2009, 00:27

woooooh
je vais faire plein de preuves constructives

c'est bon les hypersandwiches

Faut supposer des trucs sur les partitions des ingrédients ? A part mesurabilité ?

par **Nightmare** » 13 Jan 2009, 00:34

Héhé désolé de t'avoir sorti de ton lit Joker :lol3:

Doraki > Juste la mesurabilité des ingrédients.

(Je précise quand même, j'utilise le préfixe "hyper" juste pour que l'énoncé soit bien débile, mais il n'a vraiment sa place que dans "hypercouteau")

:happy3:

par **Nightmare** » 13 Jan 2009, 16:34

Pas de boulangers par ici ? :lol3:

par **skilveg** » 13 Jan 2009, 18:23

Ca rappelle un peu le théorème de Borsuk-Ulam, mais on n'a pas suffisamment de régularité... a priori. (J'aurais considéré une sphère centrée en un point du sandwich et le contenant, et l'application qui à un point de la sphère associe les mesures des différents ingrédients de la demi-boule correspondante.)

par **Nightmare** » 13 Jan 2009, 18:26

Oui en gros c'est ça :happy3:

par **skilveg** » 13 Jan 2009, 18:30

Il doit bien y avoir moyen de montrer que l'application ci-dessus est continue. Et dans ce cas tout baigne.

par **Nightmare** » 13 Jan 2009, 18:33

En considérant que les ingrédients sont bornés (ce qui colle à la réalité) on a ce qu'on veut :happy3:

par **Doraki** » 13 Jan 2009, 18:53

skilveg, ça marche mais pour (n-1) ingrédients seulement (et avec "l'origine" étant un point quelconque).

Donc il faut plonger nos demi-espaces dans R^(n+1) / R+*, homéomorphe à S^(n ou n+1 selon votre convention favorite)
On peut alors utiliser le théorème avec n ingrédients, sauf que, en cas de malchance extrême, le point obtenu peut ne pas correspondre à un demi-espace obtenu avec un hyperplan, mais à {x / 0 > 1} et {x / 0 < 1}
Or, ça c'est pas possible, y'en a un qui représente l'espace R^n tout entier et l'autre l'ensemble vide, et à moins que le sandwich soit de mesure nulle (hypothèse on ne peut plus ignoble) auquel cas n'importe quel hyperplan convient, ce n'est pas possible donc le théorème nous donne un vrai hyperplan.

par **skilveg** » 13 Jan 2009, 19:17

Oui enfin sauf erreur de ma part l'énoncé donne

ingrédients.

par **Doraki** » 13 Jan 2009, 19:31

Ah ouais.

Ca doit être parceque ma convention dit que le pain est un ingrédient supplémentaire.

par **Nightmare** » 13 Jan 2009, 19:33

Oui, c'est pour ça que j'ai modifié mon post hier, en gros le sandwich est composé de deux tranches de pain (qu'on assimile à un espace mesurable disconnexe) et de n-1 ingrédients

par **skilveg** » 13 Jan 2009, 19:47

Oui, donc, que le pain soit un des

ingrédients ou qu'il compte pour du beurre, ça marche pareil, non?

par **Nightmare** » 13 Jan 2009, 19:56

Non il faut automatique n espaces. Donc soit n-1 ingrédient plus du pain considéré comme un seul espace, soit n-2 ingrédient + deux tranches de pains, soit n ingrédients en comptant le pain comme un ingrédient.

par **skilveg** » 13 Jan 2009, 20:00

Donc Doraki a raison non? Avec n ingrédients on ne peut pas utiliser Borsuk-Ulam... Je dois être obtus...

par **Nightmare** » 13 Jan 2009, 20:01

avec n ingrédients + du pain non ça ne marche comme il l'explique.

par **ThSQ** » 14 Jan 2009, 19:04

Par hypercouteau tu sous-entends hyperplan j'imagine (pas d'hypercourbes (dommage ...))

Et faut pas que tous les hyperingrédients soient tous co-hyperplanaires.

par **Nightmare** » 14 Jan 2009, 19:12

Effectivement ThSQ, pour les hyperingrédients pas de conditions sur eux, ce sont justes des sous-espaces mesurables (au sens de Lebesgue) de R^n

Découpage d'un hypersandwich

Découpage d'un hypersandwich

Qui est en ligne