A*cos(x)+B*sin(y)

[Arsou]

Bonjour ,
Actuellement en école d'ingénieur genie électrique, j'effectue mon stage en entreprise. Je traite un sujet sur la prediction du niveau de bruit en charge d'un moteur élèctrique . Pour celà je travail sur les forces magnétomotrices crées au Stator et au rotor d'un moteur. Que je vais additionner puis multiplier par la pérmeance afin d'obtenir mon induction dans l'entrefer.

Le problème c'est que je n'arrive pas à additionner ma forcemagnétomotrice(FMM) stator avec celle crée au rotor
En effet , j'obtiens un terme pour ma FMMstator de la forme A*cos(x) et un terme FMMrotor B*sin(y)
J'essaie donc de faire l'addition de ces deux forces de telles façon à n'obtenir plus qu'un cosinus ou sinus avec une amplitude .
Soit : A*cos(x)+B*sin(y) = C*cos(z) ou sin(z)
Je ne trouve rien sur internet celà est-il possible au moins???
J'ai essaie avec les exponentielles (formules d'Euler) et trigonométrique, mais je tourne en rond :mur: .

Vous pouvez peut être m'aiguiller ?

Cordialement , Alexis.

[cuati]

Bonjour,
c'est assez connu, tu écris :
et là tu remarques que la somme des carrés des coefficients et est égales à 1, on peut donc choisir tel que et
Donc finalement :
où

[C.Ret]

Bonjour,

Je n'ai pas compris comment le terme en y disparait dans la dernière égalité :

?

IL est clair que :


mais à condition que les sin et cos de l'équation de départ soient en phase (même argument x).

Dans notre cas, stator et rotor sont en léger décallage de phase (avance de phase généralement réglable sur ce type de moteur pour contrôler la puissance ou le couple), d'où la notation utilisant x et y.

A mon avis, il faudrait faire intervenir la relation entre x et y. En général sur les moteurs à commande continue, cette relation est caractéristique du moteur (ou de son ordre de marche).

[cuati]

Bonjour,

Je n'ai pas compris comment le terme en y disparait dans la dernière égalité :

?

IL est clair que :


mais à condition que les sin et cos de l'équation de départ soient en pahse (même argument x).

Dans notre cas, stator et rotor sont en légerr décallage de phase (avance de phase généralement réglable sur ce type de moteur pour contrôler la puissance ou le couple), d'où la notation utilisant x et y.

A mon avis, il faudrait faire intervenir la relation entre x et y. En général sur le smoteur à commende analogique, cette relation est caractéristique du moteur (ou de son ordre de marche).

Oui, évidemment c'est une coquille de ma part j'ai juste mal lu l'énoncé et me suis précipité sur cette réponse... :zen:
Effectivement, avec une relation entre x et y ce sera plus facile...

[Arsou]

Effectivement j'avais aussi essaié dans ce sens , mais je n'abouti sur aucune solution. A croire que ce n'est pas possible pourtant il me parait logique que l'addition de deux signaux sinusoidaux donne un signal sinusoidale lui aussi, de fréquence et d'amplitute différente, il est donc normallement possible de le mettre sous une forme C*cos(Z) ou C*sin(Z) ...

[C.Ret]

Oui, effectivement la solution préconisée par cuati doit être la bonne.

En général, les moteurs de ce type fonctionne avec une avance/retard de pahse constante, c'est à dire que la relation entre x et y est du type x=y + theta où \théta\ exprime l'avance (ou retard) par un angle.

Dans ce cas, la solution proposée par cuati est la bonne. On peut soit trouver une phase moyenne x + \theta\ + \phi qui tient compte du décallage de phahe global ;

Soit, considérer qu'il y une perte systèmatique de puissance (proportionnelle au décallage entre x et y).
Dans ce cas, on utilisera une formule du type où le pramètre \ro vient exprimer l'effet de l'avance/retard de phase sur le rendemetn du moteur.

Mais ces deux approches ne seront valable que pour un calcul global.

Il est clair que s'il s'agit de bien qualifier le comportement du moteur lors d'un changement de régime, d'un démarrage ou d'un arrêt, ce type d'approche globale n'est pas efficace.

Lors d'un démarrag, par exemple, on peut faire l'hypothèse que x et y sont exactemetn callés lors des premiers cycle et que le décallage apparait progressivement avec la monté en charge du moteur.

Ce qui expliquerait aussi les changements observés; consommation électrique et niveau de bruit, ...

[ThekamikazeFou]

cos x-y= cosx*cosy + sinx*siny

Dans ton cas A = cos y B = sin X

Apres essai de voir si tu peux utiliser ces formules

[Arsou]

Oui, effectivement la solution préconisée par cuati doit être la bonne.

En général, les moteurs de ce type fonctionne avec une avance/retard de pahse constante, c'est à dire que la relation entre x et y est du type x=y + theta où \théta\ exprime l'avance (ou retard) par un angle.

Dans ce cas, la solution proposée par cuati est la bonne. On peut soit trouver une phase moyenne x + \theta\ + \phi qui tient compte du décallage de phahe global ;

Soit, considérer qu'il y une perte systèmatique de puissance (proportionnelle au décallage entre x et y).
Dans ce cas, on utilisera une formule du type où le pramètre \ro vient exprimer l'effet de l'avance/retard de phase sur le rendemetn du moteur.

Mais ces deux approches ne seront valable que pour un calcul global.

Il est clair que s'il s'agit de bien qualifier le comportement du moteur lors d'un changement de régime, d'un démarrage ou d'un arrêt, ce type d'approche globale n'est pas efficace.

Lors d'un démarrag, par exemple, on peut faire l'hypothèse que x et y sont exactemetn callés lors des premiers cycle et que le décallage apparait progressivement avec la monté en charge du moteur.

Ce qui expliquerait aussi les changements observés; consommation électrique et niveau de bruit, ...

Je te remercie pour ton temps de reflexion et ta reponse , mais je travail sur les forcemagnétomotrices et en l'occurence les expressions stator et rotor sont totalement différentes car elles vont deprendre du nombres d'encoches de la géométrie des encoches , du nombre de phase ainsi que des courants dans les phases. Les expressions X et Y n'ont donc rien en commun . D'ou la difficulté :marteau:


Pour le cos x-y= cosx*cosy + sinx*siny
Dans ton A = cos y / B = sin X

Celà n'est pas possible non plus .

Merci de votre aide , je crois que je vais procéder d'une autre façon pour obtenir ce que je souhaite .

[herr_mulle]

Bonjour ,
J'ai essaie avec les exponentielles (formules d'Euler) et trigonométrique, mais je tourne en rond

Vous pouvez peut être m'aiguiller ?

.

Bonjour, avec les expo, c'est pas très compliqué. Mais attention je ne vais pas être rigoureux sur les parenthèses, je vais mettre des espaces :

Acos(x)+Bsin(y)= (A/2).(exp(ix)+exp(-ix)) + (B / 2i).(Exp(ix)-exp(-ix))
or exp(ik)=cos(k)+isin(k)
1/i = -i

On a exp(ix).(A/2 - iB/2) + exp(-ix).(A/2 + iB/2) puis on passe à l'écriture polaire pour la partie cartésienne A-iB ou A+iB

on pose tan(theta)=B/A (mais on peut discuter selon le signe de A et B)

= (1/2).racine(A^2+B^2).exp(-i.theta).exp(i.x) + (1/2).racine(A^2+B^2).exp(i.theta).exp(-i.x)

= (1/2).racine(A^2+B^2).[exp(i.(x-theta) + exp(i.(-x+theta)]]

= (1/2).racine(A^2+B^2).cos(x-theta)

:zen:

[Arsou]

Bonjour, avec les expo, c'est pas très compliqué. Mais attention je ne vais pas être rigoureux sur les parenthèses, je vais mettre des espaces :

Acos(x)+Bsin(y)= (A/2).(exp(ix)+exp(-ix)) + (B / 2i).(Exp(ix)-exp(-ix))

Il y a une erreur car y et x sont différents donc ça ne marche pas .
Cela donnerai
Acos(x)+Bsin(y)= (A/2).(exp(ix)+exp(-ix)) + (B / 2i).(Exp(iy)-exp(-iy))

Et là encore je n'ai trouvé aucune solution pour rassembler les termes.



Pour infos j'ai demandais à un chercheur en mathématique qui m'a répondu que :

A cos(x) +B cos(y) = C sin/cos(z)
A cos(x) +B cos(y) n'a aucune "périodicité" naturelle en x et y. Si x+y et x-y ne sont pas de la forme p*pi avec p rationnel alors il n'y a pas de choix "naturel" de z en fonction de A, B , x , y
Il faut avoir un lien entre X et Y pour avoir des forumles "classiques" .

En gros sans lien entre X et Y impossible de trouver une solution .

[Mathusalem]

Est-ce absolument necessaire de reduire ton expression des forces pour ce que tu dois faire ?

[Arsou]

Est-ce absolument necessaire de reduire ton expression des forces pour ce que tu dois faire ?

En faite le but été d'utiliser mes deux expressions qui sont de la forme :
A*cos(;)s* t + h*;) ) + B*sin(;)r* t + n*;) )
Avec t le temps , la position angulaire mécanique du point à l'endroit ou on veux determiner la force , h les harmoniques stator, n les harminiques rotor
Et de simplifié mon expression pour la mettre sous la forme :
Amplitude * cos ( k;)* t + m*;) ) afin de pouvoir idéntifier plus facilement les harmoniques d'espace et de temps de ma force d'entrefer (m mode de déformation , k;) la fréquence corresponde au mode ainsi que l'amplitude )
Ceci me permet d'associe chaque mode avec ça fréquence pour pouvoir les comparer plus facilement .

Mais cela n'est pas absolument necessaire c'est juste beaucoup plus pratique,
Je peux aussi effectuer la FFT sur mon signal (ce que je fais actuellement). L'inconvénient c'est qu'en effectuant la FTT d'un coter j'aurais les harmoniques de temps(Frequence) avec l'amplitude, de l'autre les harmoniques d'espace (modes) avec leurs amplitudes et il faudra donc que je m'arrange pour associer chaque mode avec leurs fréquences corresspondantes .
Car ce qui m'interesse c'est d'associer les modes avec les fréquence electrique et de les comparer avec les fréquence mécanique pour prévoir des possibles phénomènes de resonnance .

Bref merci pour vos réactions je vais me débroullier sans !

[C.Ret]

En gros sans lien entre X et Y impossible de trouver une solution .

Ce lien existe. Evidemment, on ne trouve pas dans la litterature de relation entre x et y.
Mais ce lien existe, c'est lui qui explique le comportement du moteur et sa façon de changer de régime.

On distingue en général deux régimes, le régime stationnaire; le moteur a une rotation constante (et fait un certain bruit). Sous la contrainte de son régime d'allimentation et de la charge qu'il meut, il a trouvé un point d'équilibre.

Il exite alors un lien fort entre x et y, x =y + r_st tout ce passe comme si le résultat des contraintes électriques, magnétiques et mécaniques revient à un léger décalage de phase entre stator et rotor.

Et les régimes transitoires, le plus naturel étant de considérer le régime d'accélération (montée en puissance - surtout contraint pas la puissance de l'alimentation) et celui de décéleration (chute de puissance ou entrainement cinématique du rotor - qui est surtout lié à la synergie de la charge (mécanique) mue par le moteur (le rotor).

Dans le régime transitoire, évidemment il n'y a pas de relation simple entre x et y. Car le rotor "glisse" et ne suit pas les cycles que voudrait lui imposer le "stator". Mais, ce qui se passe exactemeent dépend tout à la fois de l'inertie de la charge, de la souplesse de l'alimentation, de la qualité des deux champs magnétiques. La seule chose qui est sûre c'est que le régime évolue de secondes en secondes et que si on lui en laisse le temps on finira par obtenir un régime stationnaire.

Quoique, certains régimse stationnaires ne sont stationnaires que par paliers, il arrive que de temps en temps un petit "décrochage" se produise - le moteur se recalle - En général cela passe inaperçu, sauf que ces "recallages" peuvent avoir une incidence sur le bruit que fait le dispositif.

Ces recalages sont particulièrement audibles sur les moteurs dessinés pour du ~V/6à Hz américain lorsqu'ils sont adaptés (assez maladroitement) à nos alimentations ~/50Hz. Il y a souvent un "saut" tous les 120 cycles.

Ces quatres régimes typiques (stationaire, recallage en régime stationaire, régime transitoire de monté , régime transitoire d'arrêt/descente) sont souvent considéré pour expliquer les consommations électriques ou les puissances disponibles.

Comme ici, il s'agit d'étudier le bruit que fait le moteur, ces quatre régimes correspondent bien au quatre types de sons que l'on entend à l'utilisation d'un moteur électrique. D'ailleurs, la plupart des opérateur et utilisateur d'engin mût par la force électrique (locomotive, machine outil, tram, ...)

N'oublions pas que les sons mettent en évidence les coïncidences, interférence et que le "bruit" provient tout à la fois de l'onde fondammentale produite par les des chocs mécaniques et vibratiosn que par les harmoniques.

[herr_mulle]

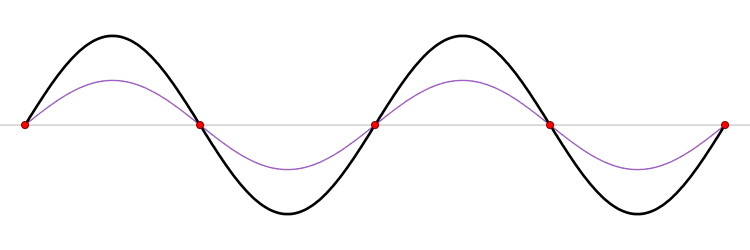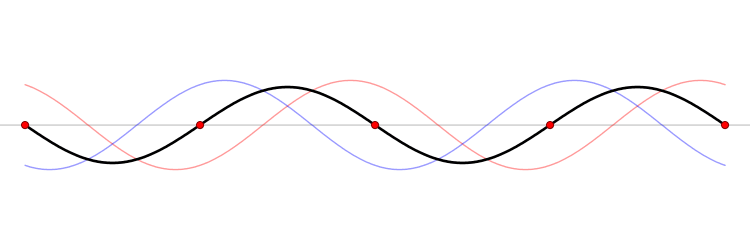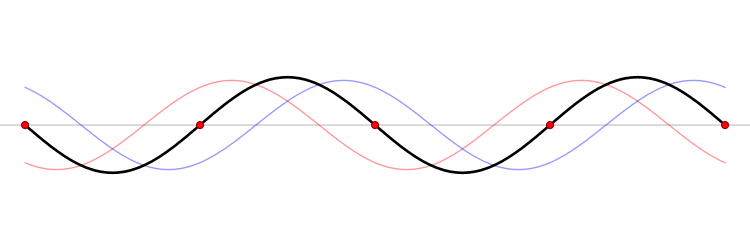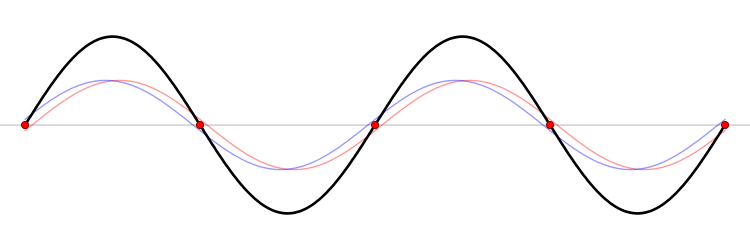
Je me suis fait avoir par de mauvaises habitudes,pour le x et y. pour vous aidez, aurait-il un moyen en utilisant des peignes de diracs (où la position entre dentures est préciser) et ensuite de prendre des produits de convotion avec la fonction Sinus. c'est une piste

Il y a une erreur car y et x sont différents donc ça ne marche pas .
Cela donnerai
Acos(x)+Bsin(y)= (A/2).(exp(ix)+exp(-ix)) + (B / 2i).(Exp(iy)-exp(-iy))

Et là encore je n'ai trouvé aucune solution pour rassembler les termes.



Pour infos j'ai demandais à un chercheur en mathématique qui m'a répondu que :

En gros sans lien entre X et Y impossible de trouver une solution .

[herr_mulle]

!

Acos(x)+Bsin(y)=

on pose y=x+phi

On a alors A'=A+Bsin(phi)= A+B.sin(y-x)
et B'=B.cos(phi)
on a A'.cos(x)+B'.sin(x) = C.cos.z

on reprend l'ancien résultat :, avec A' et B' au lieu de A et B

=(1/2).racine(A'^2+B'^2).cos(x-theta)
avec tan(theta)=B'/A'

donc C=(1/2).racine(A'^2+B'^2)

Est-ce correct ?

[C.Ret]

On pose y=x+phi

On a alors A'=A+Bsin(phi)= A+B.sin(y-x)
et B'=B.cos(phi)
on a A'.cos(x)+B'.sin(x) = C.cos.z

on reprend l'ancien résultat :, avec A' et B' au lieu de A et B

=(1/2).racine(A'^2+B'^2).cos(x-theta)
avec tan(theta)=B'/A'

donc C=(1/2).racine(A'^2+B'^2)

Est-ce correct ?

Oui, c'est le type d'expression qui traduit bien l'état stationnaire. L'abaissement de A et B en A' et B' représente bien la baisse de performance; plus le déphasage à l'équilibre est élevé, plus on s'éloigne des performances idéales du moteur (ou x et y sont parfaitement couplés).

[herr_mulle]

phi=0; donne la performance maximale (à condition que Phi soit inférieur à 90°, régime moteur) et pour phi=90°, on a une ondulation minimale.