Cos(Pi/2^n)_bis

par **mirzof** » 09 Déc 2013, 22:00

bonsoir,
je reviens vers vous pour le calcul de la valeur exacte de cos(pi/2^n).
En posant u(n)=cos(x/2^n) avec x=pi/2 et en utilisant la formule de Viète on arrive à lim(n->+inf) u1*u2*...*un=2/Pi mais je ne vois pas comment déduire la valeur exacte de u(n-1)... D'avance merci !

par **Ben314** » 09 Déc 2013, 22:07

mirzof a écrit:...je ne vois pas comment déduire la valeur exacte de u(n-1)...

Je comprend pas trop. Tu veut

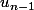
en fonction de quoi ?

Normalement, tu part de

et tu en déduit que

si

.
Ca te permet de calculer

en fonction de

.

par **mirzof** » 09 Déc 2013, 23:32

La question est de savoir comment obtenir la valeur exacte de cos(Pi/2^n).
Je peux effectivement exprimer u(n+1) en fonction de u(n) mais à partir de là comment obtenir la valeur exacte ?

par **Ben314** » 09 Déc 2013, 23:52

Si

alors

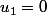
et, pour tout

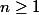
on a

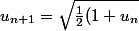donc

.
.
.

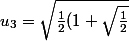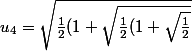voilà, ça c'est la valeur exacte de

et ça métonnerait qu'il y ait "plus simple" sans utiliser les fonction transcendantes (i.e. le sin, le cos, le ln, l'exp,...)

par **mirzof** » 11 Déc 2013, 07:55

D'accord, merci à toi !
c'est en effet ce que j'avais trouvé mais je pensais qu'on pouvait expliciter une expression de u(n) en fonction de n... :mur:

Cos(Pi/2^n)_bis

cos(Pi/2^n)_bis

Qui est en ligne