Bonjour à tous !
Je suis étudiant en Informatique et je dois programmer un petit soft de géométrie 2D qui me pose un petit problème mathématique :
Je dois être capable, à partir des coordonnées (x et y) de trois points d'un carré, de retrouver les coordonnées du quatrième point de ce carré. Ca parait tout bête et si j'avais à le faire sur une feuille je verrais bien 3-4 méthodes différentes pour le faire ! Mais ici je n'arrive vraiment pas à trouver l'équation qui va bien, qui me donnerait l'abscisse et l'ordonnée du quatrième point simplement en fonction des coordonnées des autres points.
Merci de vos lumières !
Coordonnées du quatrième point d'un carré
2 messages
- Page 1 sur 1
salut,
tu as les points
\\<br />X_1(x_1;y_1)\\<br />X_2(x_2;y_2)\\)
deja, il faut determiner quels sont les points qui sont adjacents.
//si est plus proche de
est plus proche de 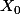 que
que 
si<d(X_0,X_2))
//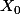 et
et  sont adjacents,
sont adjacents, 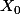 et
et  sont sur la diago, et
sont sur la diago, et  et
et  sont adjacents
sont adjacents
alors
//on va choisir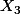 equidistant de
equidistant de 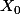 et
et 
sinon //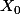 et
et  adjacents et X_1[/TEX] et
adjacents et X_1[/TEX] et  sont adjacents,
sont adjacents,
//on va choisir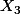 equidisant de
equidisant de  et
et 
Ensuite, on va déterminer les cordo du point) en fonction des trois autres points.
en fonction des trois autres points.
Virtuellement, on va placer le carré comme ca nous arrange.
On décide que le point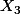 est en bas a droite. En bas a gauche c'est le point
est en bas a droite. En bas a gauche c'est le point  , en haut a gauche le point
, en haut a gauche le point  , et en haut a droite le point
, et en haut a droite le point 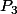 . (c'est les
. (c'est les  , mais comme vu précédemment, pas forcément aux même indices).
, mais comme vu précédemment, pas forcément aux même indices).
A partir de là, bon sans optimisation :
le point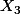 est equidistant de
est equidistant de  et
et 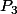 , et a une distance
, et a une distance ) de
de 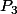 .
.
On cherche donc a résoudre le système :
=a\\<br />d(P_3,X_3)=a)
soit :
^2+(y_3-y_p_1)^2=a^2\\<br />(x_3-x_p_3)^2+(y_3-y_p_3)^2=a^2)
Bon, on s'en sort mais ya mieux.
On va tracer le vecteur . On sait déterminer un vecteur qui lui est orthogonal.
. On sait déterminer un vecteur qui lui est orthogonal.
Nos points et
et 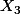 seront sur la diago dirigée par ce vecteur. la "droite" aura une equ type
seront sur la diago dirigée par ce vecteur. la "droite" aura une equ type  que ou tu détermines
que ou tu détermines  avec
avec  .
.
On remplit la condition=a^2) , on trouve surement deux solutions.
, on trouve surement deux solutions.
On garde celle ou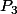 est a une distance
est a une distance  de
de 
tu as les points
deja, il faut determiner quels sont les points qui sont adjacents.
//si
si
//
alors
//on va choisir
sinon //
//on va choisir
Ensuite, on va déterminer les cordo du point
Virtuellement, on va placer le carré comme ca nous arrange.
On décide que le point
A partir de là, bon sans optimisation :
le point
On cherche donc a résoudre le système :
soit :
Bon, on s'en sort mais ya mieux.
On va tracer le vecteur
Nos points
On remplit la condition
On garde celle ou
la vie est une fête 
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
