Salut,
Si tu cherche une "astuce" rendant les calculs assez simples, je te suggèrerais bien de considérer
={2n\choose n}4^{-n}\sqrt{n+a}\)
avec

.
On a alors, pour tout

,
>w_n(a)\ \Leftrightarrow\ \frac{(2n+2)(2n+1)}{(n+1)^2}\sqrt{n+1+a}(2n+2)^2(n+a))
n^2+(5+4a)n+1+a>4n^3+(8+4a)n^2+(4+8a)n+4a)
n>3a-1)
Si

cette inégalité est vraie pour tout

et la suite correspondante est croissante donc ta suite
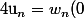)
est croissante ainsi que la suite très intéressante
)
(dans ce cas, clairement,

est très très proche de

)
Par contre, si

alors
> w_n(a)\Leftrightarrow n<\frac{1-3a}{4a-1}\)
donc la suite

est décroissante à partir d'un certain rang donné par la formule, voire même dès le premier terme si on prend par exemple

.
Enfin, de façon triviale, si

on a
<w_n(b))
et
}{w_n(b)}=1)
donc, les suites
)
et
)
sont adjacentes (éventuellement pour

) et tendent donc toutes vers la même limite
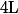
ce qui permet d'encadrer
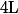
avec la précision souhaitée.

