Complexes prépa (avec balises TEX)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
blitzen
- Messages: 2
- Enregistré le: 26 Juil 2012, 00:34
-
 par blitzen » 26 Juil 2012, 01:02
par blitzen » 26 Juil 2012, 01:02
Bonjour
Quelqu'un peut-il m'aider ...
la question est de vérifier que (E):
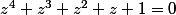
avec
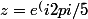)
la correction dit: comme la somme de toutes les racines 5-ième de 1 est nulle, on a bien (E) qui est vérifiée et je ne comprends pas cette explication.
Merci d'avance.
-
darkpseudo
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Juil 2010, 16:22
-
 par darkpseudo » 26 Juil 2012, 02:02
par darkpseudo » 26 Juil 2012, 02:02
Bonsoir.
Pas la peine de faire deux sujet pour une même question, tu peux voir ta somme comme la somme de termes d'une suite géométrique de raison z.
-
Hiruma
- Messages: 4
- Enregistré le: 23 Juil 2012, 11:51
-
 par Hiruma » 26 Juil 2012, 09:16
par Hiruma » 26 Juil 2012, 09:16
Bonjour,
Comme tu ne comprends pas l'explication que l'on t'a fourni il peut également être intéressant pour toi de généraliser ce résultat en redémontrant que la somme des racines n-ième de l'unité est égale à 0
Pour se faire, tu peux poser
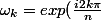=exp(\frac{i2\pi}{n})^k)
et calculer
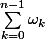
comme on te l'a dit, en utilisant les suites géométriques
-
TekMath
- Membre Naturel
- Messages: 10
- Enregistré le: 23 Juil 2012, 13:59
-
 par TekMath » 27 Juil 2012, 04:46
par TekMath » 27 Juil 2012, 04:46
Il faut déjà savoir ce que sont les racines cinquième de l'unité. Ce sont les solutions de l'équation:

Par exemple les racines carrées de l'unité sont -1 et +1:

Dans le cas de la première équation le théorème fondamental de l'algèbre te donne le résultat suivant:
Pour un polynôme de degré cinq il y a cinq racines, pas forcément distinctes.Je te laisse chercher comment on trouve ces 5 racines, tu dois trouver le nombre z donné par ton énoncé. Ensuite, la question est de savoir pourquoi la somme des cinq nombres complexes qui vérifient cette équation se trouve être nulle.
La réponse tient dans la relation coefficients-racines: Le polynôme (X^5-1) dont les cinq solutions sont 1 puis z puis le carré de z puis son cube et enfin z^4 s'écrit sous forme factorisée. Il te reste à développer cette forme et comparer avec (X^2-1).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités