Arctangente

[Raphoul]

bonjour,
je devais montrer que :

et
je l'ai fais sa
ensuite je devais calculer
j'ai trouver que cela faisait 0
et ensuite je dois en déduire la valeur de
je suis bloquer ici

[Gonra]

Salut ,
si , quelles sont les valeurs pour lesquelles le cosinus s'annule ?

[Raphoul]

Salut ,
si , quelles sont les valeurs pour lesquelles le cosinus s'annule ?

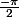
et ?

[Gonra]

Donc pour x>0 ......
et Pour x<0 ......

[siger]

bonsoir

1 + tan^2(a) = 1/cos^2(a)
a = arctan(x) ou x = tan(a)
cos^2(a) = 1/(1+x^2))
.....

[Raphoul]

[quote="Gonra"]Donc pour x>0 ......
et Pour x0 ca vaut pi/2 et pour x<0 ca vaut -pi/2
c'est sa ?

[Raphoul]

c'est sa ou pas ?

[Gonra]

C'est bien ça.
bonne soirée

[Raphoul]

je dois résoudre sur

comment commencer cette résolution ?

[Gonra]

1) Soit tu pose
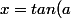2) Soit tu montre que la fonction est constante en dérivant puis tu sauras que

si tu optes pour la 1er méthode , il faudrait que tu saches que

[Raphoul]

je penser calculer la dériver d'abord et trouver 0 comme sa la fonction serai constante et trouver f(0) =pi/2 ?

[Gonra]

exactement

[Ben314]

Salut,
Y'a un truc que je capte pas trop dans ce fil....

Si j'ai tout bien lu, on demandé à Raphoul dans un premier temps de montrer que :
- Pour tout réel x>0
- Pour tout réel x<0

Plus plus tard, on demande au même Raphoul de
"résoudre sur l'équation "

bizarre bizarre
(Moi, j'ai dit bizarre, bizarre, comme c'est étrange ! Pourquoi aurais je dit bizarre, bizarre ?)

[Raphoul]

Salut,
Y'a un truc que je capte pas trop dans ce fil....

Si j'ai tout bien lu, on demandé à Raphoul dans un premier temps de montrer que :
- Pour tout réel x>0
- Pour tout réel x<0

Plus plus tard, on demande au même Raphoul de
"résoudre sur l'équation "

bizarre bizarre
(Moi, j'ai dit bizarre, bizarre, comme c'est étrange ! Pourquoi aurais je dit bizarre, bizarre ?)

merci de cette réponse ben314, je me suis tromper en lisant l'énoncer je dois résoudre sur l'équation

[Raphoul]

et donc je trouve x=pi/4

[Gonra]

Salut ,

tu essayes de résoudre quoi du coup ?

[Ben314]

A mon avis celle là : :zen:

et donc je trouve x=pi/4

Et çe n'est pas la bonne réponse.
Quelle démarche as-tu suivi ? (plusieurs possibilités dont une particulièrement rapide...)

[Raphoul]

A mon avis celle là : :zen:


Et çe n'est pas la bonne réponse.
Quelle démarche as-tu suivi ? (plusieurs possibilités dont une particulièrement rapide...)

j'ai composer par tangente

[Raphoul]

ou je dois pas faire comme sa ?

[Raphoul]

une petite aide svp ?