Arctangente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Fév 2006, 23:20
par yos » 21 Fév 2006, 23:20
Je me permets de ressortir une question qui est passée hier. Je ne sais pas pourquoi le post a été fermé. Je trouve que c'est tout de même intéressant.

sont des réels tels que

.
Montrer qu'il existe (i,j) tel que

-
redwolf
- Membre Relatif
- Messages: 115
- Enregistré le: 08 Fév 2006, 11:00
-
 par redwolf » 21 Fév 2006, 23:27
par redwolf » 21 Fév 2006, 23:27
Ah ! Je suis content que quelqu'un ressorte la question, parce que j'y ai passé une bonne heure et j'ai même tapé ma solution tellement je trouvais le problème sympathique. Par contre, je ne sais pas comment afficher un document pdf tout prêt, ou entrer mon source TeX sans changer tous mes $ en [TeX].
-
redwolf
- Membre Relatif
- Messages: 115
- Enregistré le: 08 Fév 2006, 11:00
-
 par redwolf » 21 Fév 2006, 23:33
par redwolf » 21 Fév 2006, 23:33
Mais bien sur, le titre du message de Yos vient de me faire trouver une solution à peu près dix fois plus courte que la mienne. Je me tairai donc sur ce sujet.
A+
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 22 Fév 2006, 11:00
par El_Gato » 22 Fév 2006, 11:00
Une solution serait la bienvenue. J'ai cherché 20 minutes et j'ai pas trouvé.
Merci
-
redwolf
- Membre Relatif
- Messages: 115
- Enregistré le: 08 Fév 2006, 11:00
-
 par redwolf » 22 Fév 2006, 11:29
par redwolf » 22 Fév 2006, 11:29
Bon, alors je m'y colle quand même :
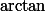
réalise une bijection de

sur
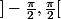
. Appelons

les images des

. La quantité

n'est autre que
)
, et
<\frac{1}{\sqrt{3}})
équivaut à

. Il s'agit donc de démontrer que parmi sept nombres de
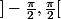
, il y en a deux dont la distance est strictement inférieure à
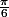
.
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 22 Fév 2006, 11:30
par El_Gato » 22 Fév 2006, 11:30
redwolf a écrit:Bon, alors je m'y colle quand même :
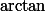
réalise une bijection de

sur
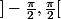
. Appelons

les images des

. La quantité

n'est autre que
)
, et
<\frac{1}{\sqrt{3}})
équivaut à

. Il s'agit donc de démontrer que parmi sept nombres de
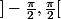
, il y en a deux dont la distance est strictement inférieure à
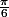
.
Merci bien !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
 sont des réels tels que
sont des réels tels que  .
.
