Arctan(x)+arctan(1/x)

[qaterio]

Bonjour, j'aurai aimé savoir si ma démonstration était correcte (ça fait aprtie d'un DM, il faut que toutes les justifications soient parfaites alors je prends toutes les critiques !):
Merci d'avance.

[Carpate]

C'est peu lisible et ne donne pas envie de l'examiner.
Peux-tu taper le texte au clavier ?

[Black Jack]

Salut,

Tu donnes une résolution de problème ... dont on ignore l'énoncé.

Je présume qu'il s'agissait de trouver un équivalent à f(x) = arctan(x) + arctan(1/x)

Je ne vois nulle part le domaine d'existence mentionné dans ce que tu as écrit ...

Je te proposerais de trouver ce que vaut f'(x).

f'(x) = ...

Et d'en tirer les conséquences en tenant compte du domaine d'existence de f(x).

[Ben314]

Salut,
C'est pas terrible ton truc.
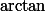
Déjà, c'est pas une fonction, c'est un réel (qui dépend du réel ). la fonction c'est tout seul. De même, c'est pas une fonction. la fonction c'est .
Et de confondre les deux, ça va rapidement te planter (en particulier pour tout ce qui est composition, substitution et/ou dérivation)

Et d'ailleurs j'ai jamais compris pourquoi on laissait alègrement les lycéens confondre les deux : est-ce que c'est vraiment trop compliqué pour nos chères "tètes blondes" de comprendre qu'une cafetière (=machine à faire du café) et du café (=ce qui sort de la machine), c'est pas la même chose ?

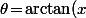Sinon, le milieu est à peu prés là, mais c'est quand même super lourd comme écriture : tu aurais posé une bonne fois pour toute pour un réel fixé que ça aurait grandement gagné en clarté.

Par contre la fin, c'est n'importe quoi : ça m’intéresserait fortement de savoir quel raisonnement te conduit à penser qu'il y a un quelconque rapport entre le fait que soit strictement positif et le fait que .

[mathelot]

si

d'où
si



soit



pour

[qaterio]

Bonjour,
j'ai pris compte de vos commentaires, je vais arranger tout ça.
Merci beaucoup.

[qaterio]

Bonjour,
est-ce que c'est mieux ? je l'ai fait de deux manières différentes dont l'une similaire à la première mais j'ai essayé de tenir compte de vos commentaires.
https://postimg.cc/6TCHPT3S/33e02d53
https://postimg.cc/4mNShsfS/c13f7735

[mathelot]

Avec la dérivée nulle , on montre que la fonction
est constante sur et sur (i.e,les deux composantes connexes de )

[qaterio]

Oui mais elle pourrait très bien faire comme la fonction partie entière qui a une dérivée nulle..
Après je en comprend peut-être pas le terme : "les deux composantes connexes de R*".

[mathelot]

un espace topologique connexe est un espace d'un seul morceau, d'un seul tenant.
Précisément, il ne peut être recouvert par la réunion d'ouverts non vides et disjoints deux à deux
La composante connexe d'un point est le plus grand connexe contenant ce point.
ici, a deux composantes connexes qui sont les intervalles et

[qaterio]

D'accord, je commence la topologie au S2, c'est pour bientôt !
Mais du coup, c'est bon ce que j'ai mis ici ? https://postimg.cc/4mNShsfS/c13f7735

[mathelot]

D'accord, je commence la topologie au S2, c'est pour bientôt !
Mais du coup, c'est bon ce que j'ai mis ici ? https://postimg.cc/4mNShsfS/c13f7735

non, ce n'est pas bon. Il faut écrire f est constante sur R+* et f est constante sur R-*
( ce n'est pas la même constante)