Arcsinx
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
SawcenMS
- Membre Naturel
- Messages: 16
- Enregistré le: 12 Déc 2014, 13:16
-
 par SawcenMS » 12 Déc 2014, 13:25
par SawcenMS » 12 Déc 2014, 13:25
comment montrer que :
arcsin;)x -(1/2)arcsin(2x-1) = ;)/4 ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 12 Déc 2014, 13:31
par chan79 » 12 Déc 2014, 13:31
SawcenMS a écrit:comment montrer que :
arcsin;)x -(1/2)arcsin(2x-1) =

/4 ?
salut
Dérive le premier membre
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 12 Déc 2014, 15:39
par Pythales » 12 Déc 2014, 15:39
SawcenMS a écrit:comment montrer que :
arcsin;)x -(1/2)arcsin(2x-1) =

/4 ?
Pose

-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 12 Déc 2014, 18:10
par paquito » 12 Déc 2014, 18:10
chan79 a écrit:salut
Dérive le premier membre
Si tu poses
=arcsin{sqrt{x}}-\frac{1}{2}arc sin (2x-1))
, tu vas trouver rapidement f'(x)=0, ce qui résout rapidement le problème!
-
SawcenMS
- Membre Naturel
- Messages: 16
- Enregistré le: 12 Déc 2014, 13:16
-
 par SawcenMS » 12 Déc 2014, 21:52
par SawcenMS » 12 Déc 2014, 21:52
g dérivé mais j'arrive jamais a 0 :
f'(x)=(1;)(2;)x))×(1;);)(1;)x²)) ;) 1;);)(1;)(2x;)1)²) g continué de développer la dérivée mais ça ne se résoud pas -_-

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 12 Déc 2014, 22:18
par Sa Majesté » 12 Déc 2014, 22:18
Tu t'es trompé dans la dérivée de

-
SawcenMS
- Membre Naturel
- Messages: 16
- Enregistré le: 12 Déc 2014, 13:16
-
 par SawcenMS » 12 Déc 2014, 22:54
par SawcenMS » 12 Déc 2014, 22:54
Sa Majesté a écrit:Tu t'es trompé dans la dérivée de

la dérivée de cette fonction est: la dérivée de

x * la dérivée de arcsinx appliquer en

x :
et (arcsinx)'= 1/;)(1-x²), ou je me suis trompé?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 12 Déc 2014, 23:02
par Sa Majesté » 12 Déc 2014, 23:02
SawcenMS a écrit:la dérivée de cette fonction est: la dérivée de

x * la dérivée de arcsinx appliquer en

x :
et (arcsinx)'= 1/;)(1-x²), ou je me suis trompé?
Ici : la dérivée de arcsinx appliquée en

x
-
SawcenMS
- Membre Naturel
- Messages: 16
- Enregistré le: 12 Déc 2014, 13:16
-
 par SawcenMS » 12 Déc 2014, 23:46
par SawcenMS » 12 Déc 2014, 23:46
Sa Majesté a écrit:Ici : la dérivée de arcsinx appliquée en

x
ok stp donne moi la solution :lol3:
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 13 Déc 2014, 09:04
par paquito » 13 Déc 2014, 09:04
=\frac{1}{2\sqrt{x}}\frac{1}{sqrt{1-x}}-\frac{1}{sqrt{-4x^2+4x}})
et
^2)
; il faut distinguer les cas

-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 13 Déc 2014, 09:05
par BiancoAngelo » 13 Déc 2014, 09:05
SawcenMS a écrit:ok stp donne moi la solution :lol3:
Réfléchis deux secondes avant de dire "donne moi la solution", car la solution vient de t'être donnée.
La dérivée de x-> arcsin(x) est ........... , et on remplace x par racine(x)... pour avoir la dérivée de Arcsin(racine(x)) qui est bien le produit de la dérivée de l'intérieur par la dérivée de Arcsin appliquée à l'intérieur (ici l'intérieur est racine x...).
Il faut correctement appliquer la formule (v(u(x)))' = u'(x) * v' (
u(x)).
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 13 Déc 2014, 09:07
par BiancoAngelo » 13 Déc 2014, 09:07
paquito a écrit:=\frac{1}{2\sqrt{x}}\frac{1}{sqrt{1-x}}-\frac{1}{sqrt{-4x^2+4x}})
et
^2)
; il faut distinguer les cas

Ah bon,

est définie si x < 0 ? :triste:
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 13 Déc 2014, 09:11
par BiancoAngelo » 13 Déc 2014, 09:11
paquito a écrit:=\frac{1}{2\sqrt{x}}\frac{1}{sqrt{1-x}}-\frac{1}{sqrt{-4x^2+4x}})
et
^2)
; il faut distinguer les cas

Parce que, sous la deuxième racine, en factorisant par 4... et par x...
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 13 Déc 2014, 09:12
par paquito » 13 Déc 2014, 09:12
paquito a écrit:=\frac{1}{2\sqrt{x}}\frac{1}{sqrt{1-x}}-\frac{1}{sqrt{-4x^2+4x}})
et
^2)
; il faut distinguer les cas

Non bien sûr, f 'est définie pour x>0; c'est
^2)
qui demanderait des précautions inutiles ici; désolé, j'ai écrit trop vite!
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 13 Déc 2014, 09:14
par paquito » 13 Déc 2014, 09:14
BiancoAngelo a écrit:Parce que, sous la deuxième racine, en factorisant par 4... et par x...
oui, ça se simplifie.
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 13 Déc 2014, 09:19
par BiancoAngelo » 13 Déc 2014, 09:19
paquito a écrit:oui, ça se simplifie.
Pour ma part, j'ai souvent le même réflexe que toi, dès que j'ai racine au carré ou carré de la racine, je me dis "Attention !" alors que le premier cas n'a pas besoin d'être détaillé.
Mais au moins, on fait attention :ptdr:
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 13 Déc 2014, 09:36
par paquito » 13 Déc 2014, 09:36
f(x) est définie ici pour

et (
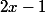 \in [-1; 1])
donc on aura
 =\frac{\pi}{4})
sur

on trouve

pour x=0 ou x=1 ou x= 1/2 etc...
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 13 Déc 2014, 09:42
par Pythales » 13 Déc 2014, 09:42
SawcenMS a écrit:comment montrer que :
arcsin;)x -(1/2)arcsin(2x-1) =

/4 ?

soit

=t-\frac12arcsin(-cos2t)=t-\frac12(2t-\frac{\pi}2)=...)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Déc 2014, 12:51
par Ben314 » 13 Déc 2014, 12:51
C'est plus rapide (et plus joli a mon avis), mais
attention a bien tout
justifier...
On y gagne en calcul en évitant les dérivée, mais on y perd (un peu) en justifications concernant l'intervalle dans lequel on a pris le t pour justifier que,
pour les t dans cet intervalle là, on a bien Arcsin(sin(t))=t ainsi que arcsin(-cos(2t))=2t-pi/2 (formules clairement fausses pour des réels t quelconques)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 13 Déc 2014, 13:19
par Pythales » 13 Déc 2014, 13:19
Ben314 a écrit:C'est plus rapide (et plus joli a mon avis), mais attention a bien tout justifier...
On y gagne en calcul en évitant les dérivée, mais on y perd (un peu) en justifications concernant l'intervalle dans lequel on a pris le t pour justifier que, pour les t dans cet intervalle là, on a bien Arcsin(sin(t))=t ainsi que arcsin(-cos(2t))=2t-pi/2 (formules clairement fausses pour des réels t quelconques)
Il est clair que

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
soit

