Application du théorème des noyaux

[pihro]

Bonjour,

j'ai un peu de mal à répondre à ce qui suit :

Soit M une matrice 3x3 non nulle telle que M^3 = -M
En appliquant le théorème des noyaux, montrer qu'il existe P tel que

[yos]

Si ta matrice est complexe, c'est faux (exemple : matrice diag(i,i,i)). Donc je suppose que M est réelle.
M est annulée par qui se factorise en et les deux facteurs sont premiers entre eux. Le th des noyaux dit que est somme directe des noyaux de M et (j'identifie la matrice M et l'endomorphisme m de qu'elle représente dans la base canonique). Le déterminant de M est un réel solution de , donc il vaut 0. Ainsi le noyau de M est de dimension au moins 1. Il ne peut pas être de dimension 3 (sinon la matrice serait nulle) ni de dimension 2 (sinon ... je vais y réfléchir).

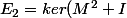Ainsi est de dimension 2. On construit une base de dans laquelle M a pour matrice
000
00-1
010
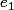
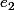
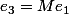
Pour cela on prend un vecteur non nul du noyau de M (le premier élément de la base), et un vecteur non nul de et on pose . On vérifie facilement que est libre (donc une base) et que la matrice de M dans cette base est celle voulue.

[yos]

Je bouche le trou : est stable par M et donc s'il était de dimension 1, ça ferait un espace propre de dimension 1, ce qui est impossible car 0 est la seule valeur propre de M (dans R) et les vecteurs propres associés à 0 sont dans et donc pas dans .
J'espère que tu pourras reconstituer la preuve (plus facile qu'elle en a l'air mais assez constructive)

[pihro]

merci beaucoup pour votre réponse

Il reste cependant un point que j'ai mal compris : à quoi sert ici le théorème des noyaux ?

[Zebulon]

Bonjour,
on applique le théorème des noyaux aux polynômes X et X²+1 pour montrer que ce qui permet d'obtenir pour base de une base contituée de vecteurs propres de M dans Ker(M) juxtaposée à une base de vecteurs propres de M dans Ker(M²+1).

[pihro]

merci beaucoup, j'ai compris maintenant l'intérêt du théorème !