Application

[abicah]

Bonsoir,

Soit une application f : E---> F

On suppose que quelque soit A appartenant à P(E) .
Comment fait t on pour démontrer que pour tout ensemble A et B de P(E) f(A)n f(B) c f(AnB)
mais uniquement en substituant les ensembles par leur définition de départ (si c'est possible)?

j'ai essayé en démarrant comme ca mais je n'arrive pas à aboutir au résultat

Merci

vam edit > en Ltx, l'intersection se code par \cap

[catamat]

Bonjour
Soit y un élément de f(E) et x un antécédent de y par f,
Posons A={x}
donc f(A)={y}
Par hypothèse, l'image réciproque de [y} est égale à A donc {x}.
y est donc le seul antécédent x par f.

Donc tout élément de f(E) admet un et un seul antécédent.

Soit z élément de (supposé non vide)
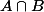
Par f, z a un antécédent dans A et un antécédent dans B, mais comme par hypothèse z a un seul antécédent celui ci est dans , donc z est élément de

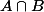
De plus si est vide alors est vide et aussi

[abicah]

Bonjour ,

Merci pour ton retour .
Ta démonstration est correct mais tu utilises des variables (x, y , z ) pour la démonstration ,
ce que je souhaite justement éviter .