Actions de groupe

[RadarX]

Bonjour,
Je vous met d'abord un peu dans le bain.

Si un groupe G agit sur un ensemble X, alors Gx {gx/ g€G} est appelé orbite de x sous G; à différencier de G indice(x)= {g€G/ gx=x} qui est appelé le fixateur de x dans G (c'est alors un sous groupe de G).

Alors dans le cours d'un prof il est marqué que:
G indice(gx) = g G indice(x) g^1 (preuve facile et je peux la donner si ca interesse qqu'un). Mais il ajoute "et inversement" cad que si G indice(y) = g G indice(x) g^1 alors y = gx. Ce qui s'avère etre faux et il a reconnu l'erreur.

Il ajoute toujours l'equivalence suivante qu'il a reconnu fausse car ce qui precede est faux:
La donnée de X où G agit transitivement (ie G\X = {X}) équivaut a celle d'une classe de conjugaison de sous groupes de G.
mais le justifie avec le contre exemple suivant (copier-coller de son mail):

Pour s'en convaincre, il suffit de prendre G commutatif (exemple G=IR) agissant sur X = S^1 (le cercle) par rotation: g.e^{2i\pi t} := e^{2 i \pi (t + g)} : l'action est transitive, et le stabilisateur de tout point x de S^1 est le sous-groupe Z de IR qui n'a que lui-meme comme conjugue.

Question 1: pouvait me donner une def claire de ce cercle S^1 (que je pense etre le cercle unité); Et si c'est le cercle unité pourquoi noter les elements e^(2i/pi t) au lieu de e^it (t€IR)? Quel interet de noter de la 1ere maniere?

Question 2: Que signifie action par rotation?

En Resumé: Que signifie clairement le X et comment IR agit sur ce X?

Desolé d'être long mais je voulais donner le max de details pour des reponses au max claires.

Merci de vous triturer les meninges (quoique....)
RadarX.

[ayanis]

Bonjour,

1 alors, je pense que c'est bien le cercle unité en effet et que la première notation est plus utilisée car on y voit Pi ce qui rappelle qu'on raisonne en radians. Mais ca ne chenge rien de le mettre ou pas... en revanche dans la suite il dit que " le stabilisateur de tout point x de S^1 est le sous-groupe Z de IR qui n'a que lui-meme comme conjugue." ce qui ne serait pas possible sans le 2/pi, ca deviendrait Pi/2 Z. Mais c'est pas très important...

Une action par rotation comme dit son nom est une rotation, que se passe t il quand on transforme un cercle de centre O par une rotation de centre O? Il bouge pas... je m'exprime surement mal, j'ai bien compris mais je n'arrive pas à reformuler clairement... désolée

ttyl

[RadarX]

Bonjour,

1 alors, je pense que c'est bien le cercle unité en effet et que la première notation est plus utilisée car on y voit Pi ce qui rappelle qu'on raisonne en radians... en revanche dans la suite il dit que " le stabilisateur de tout point x de S^1 est le sous-groupe Z de IR qui n'a que lui-meme comme conjugue." ce qui ne serait pas possible sans le 2/pi, ca deviendrait Pi/2 Z. Mais c'est pas très important...

Une action par rotation comme dit son nom est une rotation, que se passe t il quand on transforme un cercle de centre O par une rotation de centre O? Il bouge pas... je m'exprime surement mal, j'ai bien compris mais je n'arrive pas à reformuler clairement... désolée

ttyl

Merci, mais je reste encore perplexe.
Cercle unité confirmé, oui! Et puis en ecrivant e^{2i\pi t} ne voulait-il pas ecrire plutot e^{2i/pi t) ie exp(2i/'pi.t)} (Slash ou anti slash?)
Je continue quand meme a reflechir au bleme.

[ayanis]

"Triste Sir celui qui ne depasse pas son professeur." Da Vinci.

oui mais quand on a eu un prof ex major d'ulm, qui pond des sujets d'ens, c'est pas facile de le dépasser...

:triste:

ttyl

[RadarX]

"Triste Sir celui qui ne depasse pas son professeur." Da Vinci.

oui mais quand on a eu un prof ex major d'ulm, qui pond des sujets d'ens, c'est pas facile de le dépasser...

:triste:

ttyl

Pas facile mais pas impossible!! Il a bien reussi lui a depassé quelqu'un. Rien n'est facile Monsieur. Faut s'investir avec abnegation.
A ce propos cette autre citation de Da Vinci (decidement bien inspiré) " Quand on veut fortement, constamment on reussit toujours"; c'est à prouver mais essaye et tu verras. Donc VOLONTE ET CONSTANCE OU PERSEVERANCE. Et puis il n'est pas dit qu'on doit le depasser le prof dans son terrain; on peut realiser une oeuvre dans tout autre domaine qui vous donne beaucoup plus (sinon autant) de prestige que lui dans son domaine.
On a vu de bons eleves tres admiratifs de leurs profs de maths au lycee ou de d'anatomie a la Fac (tellement ils etaient impressionants niveau maitrise de leurs sujets et pedagogiques), devenir de grands Professeurs renommés de medecine, par dela les maths du lycee ou l'anatomie des premieres annees de Fac.
De toute facon on peut entendre cette citation de Da Vinci comme un credo qui nous pousse (nous motive toujours) a chercher davantage, a aller plus loin.

[El_Gato]

D'une manière générale, 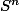est la sphère unité de . On peut donc dire que 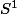, le cercle de rayon 1 dans est paramétré par avec 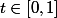ou par les avec 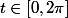, c'est pareil. D'autre part s'identifie naturellement avec la rotation d'angle t modulo 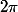. Ainsi 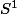s'identifie, au moins algébriquement (et aussi topologiquement) à , le groupe des rotations dans le plan.

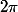Quant à l'action de groupe elle consiste à additionner l'angle de la rotation avec g modulo . Autrement dit on considère que g est un angle que l'on ajoute à la rotation de départ.

[RadarX]

D'une manière générale, est la sphère unité de . On peut donc dire que , le cercle de rayon 1 dans est paramétré par avec ou par les avec , c'est pareil. D'autre part s'identifie naturellement avec la rotation d'angle t modulo . Ainsi s'identifie, au moins algébriquement (et aussi topologiquement) à , le groupe des rotations dans le plan.

Quant à l'action de groupe elle consiste à additionner l'angle de la rotation avec g modulo . Autrement dit on considère que g est un angle que l'on ajoute à la rotation de départ.

Cette contrib m'eclaircit un peu: c'est donc le prof qui a du faire des erreurs de parametrage pour S^1.
Mais chipotons quand meme un peu (souci de rigueur), S^1 ne serait-ce pas plutot { e^it; t€ [0;2pi[ } (intervalle ouvert en 2pi et non fermé)?

Autre chose j'aimerais avoir une definition claire et formelle SO² des rotations du plan.

Gracias Gaato.

RadarX.

[quinto]

Mais chipotons quand meme un peu (souci de rigueur), S^1 ne serait-ce pas plutot { e^it; t€ [0;2pi[ } (intervalle ouvert en 2pi et non fermé)?

Non, tu peux même aller aussi loin que tu veux après 2pi, fermé ou pas, ca ne change rien parce que la fonction exponentielle est périodique.
D'ailleurs, note que S^1 n'est isomorphe à aucun compact de R, ni à aucun intervalle de R.
a+

[El_Gato]

Cette contrib m'eclaircit un peu: c'est donc le prof qui a du faire des erreurs de parametrage pour S^1.
RadarX.

Non, je ne crois pas que ton prof ait commis une erreur. La nature de l'intervalle importe peu ici. Prenons-le fermé.

est l'ensemble des matrices orthogonales de taille 2-2 et de déterminant positif, c'est à dire l'ensemble des matrices de la forme
. La loi de groupe c'est la multiplication des matrices. C'est donc l'ensemble des matrices des rotations vectorielles du plan vectoriel. L'isomorphisme avec s'obtient en identifiant avec l'ensemble des : au complexe on associe la rotation d'angle t c'est à dire la matrice de :
.
Soit cette application. On vérifie immédiatement que , donc on a bien un isomorphisme de groupes.

Sans faire de calculs, tout ceci est évident car est équivalent à la formule: lequelle revient à dire que composer deux rotations dans le plan autour de l'origine consiste à exécuter une rotation dont l'angle est la somme des deux, ce qui est évident intuitivement.

[ayanis]

est l'ensemble des matrices orthogonales de taille 2-2 et de déterminant positif, c'est à dire l'ensemble des matrices de la forme
.

Je dirai meme de déterminant égal à 1.

ttyl

[RadarX]

En fait, j'ai pensé qu'il fallait mieux ouvrir l'intervalle pour des raisons de definition d'un ensemble. En effet, un ensemble ne pouvant pas contenir 2 fois le meme element, si on ferme l'intervalle [0; ], contiendra 2 fois l'lement qui est egale a .

[quinto]

En fait, j'ai pensé qu'il fallait mieux ouvrir l'intervalle pour des raisons de definition d'un ensemble. En effet, un ensemble ne pouvant pas contenir 2 fois le meme element, si on ferme l'intervalle [0; ], contiendra 2 fois l'lement qui est egale a .

Je ne vois pas le problème:
l'ensemble {1,1} contient deux fois le nombre 1 et donc cet ensemble n'est rien autre que {1}

[RadarX]

Je ne vois pas le problème:
l'ensemble {1,1} contient deux fois le nombre 1 et donc cet ensemble n'est rien autre que {1}

Je l'ai dit dans mon message precedent, par definition, dans l'ecriture dun ensemble, chaque element n'y figure une seule fois.
Le couple , mais l'ensemble {1,1} est syntaxiquement incorrecte; on ecrit tout court {1}.
Donc ecrire un ensemble sous la forme qui y fait figurer 2 fois le meme element pose un pb de syntaxe.

[quinto]

Absolument pas !
Tu peux écrire autant de fois le même élément dans un ensemble que tu veux, ca ne veut pas dire que ton ensemble le possédera plusieurs fois et ca n'en sera pas faux pour autant.

[RadarX]

Absolument pas !
Tu peux écrire autant de fois le même élément dans un ensemble que tu veux, ca ne veut pas dire que ton ensemble le possédera plusieurs fois et ca n'en sera pas faux pour autant.

Alors peux tu me dire le card de {1,1} (son nb d'elements) et citer ses differents elements? Tu me diras peut etre card = 2 en les comptant. Et aussi le card de {1} et ses diff elements.

Par ailleurs peux tu comparer ces 2 derniers ensembles en oubliant pas que s'ils sont egaux ils doivent imperativement avoir le meme cardinal.
N'y vois tu pas un paradoxe?

[ayanis]

" * si a et b sont égaux, nous constatons que, d’après la définition, { a, a } n’est autre que le singleton { a } ;"

Pris dans wikipédia...

Désolée Radar X mais je crois que Quinto a raison.

ttyl

[RadarX]

" * si a et b sont égaux, nous constatons que, d’après la définition, { a, a } n’est autre que le singleton { a } ;"

Pris dans wikipédia...

Désolée Radar X mais je crois que Quinto a raison.

ttyl

Decidement!!! Soit, il va falloir donc que je revois ma theorie (elementaire) des ensembles.

Merci de toutes les remarques et contrib.

[RadarX]

agit sur par l'action suivante:
Si et , alors =
(Cette action est transitive, à titre informatif)

Mais on m'affirme surtout que le stabilisateur de tout x = est .
Je suis dans la demo mais, je bute encore sur la résolution de = .

cela devrait donner:
= ou = , pour le cosinus.
ET
= pour le sinus.

Ca donne ensuite apres simplifications:

ou pour le cos
ET
pour le sin.
Et cela ne me dit pas que .

Perplexe, je suis, à moins que cela ne soit encore la fatigue!

Vivement vos contib Merci.