Forum de Mathématiques: Maths-Forum

Un peu d'aide ? :)

mr_pyer a écrit: Je crains que la solution ne soit pas une série de Fourier...

Pourtant c'est bien sous cette forme qu'il faut trouver y

up :) si quelqu'un a une idée :)

Bonsoir ! Je me demandais comment résoudre à l'aide d'une série de fourier l'équa diff suivante : y'-e^{ix} y=cos(x) En passant par les coefficients de Fourier ( les cn(f) ) on obtient: \forall n \in \mathbb{N},c_n(y'-e^{ix} y)=c_n(cos(x)) soit: \forall n \in ...

jlb a écrit:Prend un contre-exemple E=R F={y tq |y-3|<1} et x=1 et si tu trouves y dans f vérifiant |y-1|=1 cela va être difficile!!

Je te remercie de ta réponse

MMu a écrit:Non ... :zen:

Comment peut-on alors le montrer ?

Bonsoir, j'aimerais une aide pour ce petit énoncé
On se donne F une partie non vide d'un espace vectoriel normé E
Soit .
Si F est un ouvert, existe-t-il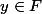 tel que
Merci à tous