20 résultats trouvés
Revenir à la recherche avancée
busard_des_roseaux a écrit:dans le terme générique de la somme, on remplace l'indice

par

c'est bien sa non ? en rajoutant un terme, pourquoi remplacer i par n+1
- par Raph1
- 01 Nov 2013, 12:22
-
- Forum: ✯✎ Supérieur
- Sujet: raisonnement par récurrence
- Réponses: 16
- Vues: 602
busard_des_roseaux a écrit:du coup, mon conseil de 11h52 reste valable...
je sais que c'est un truc comme ça mais il manque un truc que je ne trouve pas
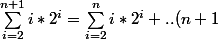)
- par Raph1
- 01 Nov 2013, 12:07
-
- Forum: ✯✎ Supérieur
- Sujet: raisonnement par récurrence
- Réponses: 16
- Vues: 602
busard_des_roseaux a écrit:le plus simple est de calculer

entre nous, pas besoin de récurrence...
c'est l'énoncé qui me le demande par récurrence et comme on a fait le cours juste avant, je dois comme ça
- par Raph1
- 01 Nov 2013, 11:58
-
- Forum: ✯✎ Supérieur
- Sujet: raisonnement par récurrence
- Réponses: 16
- Vues: 602
bonjour, je dois démontrer par récurrence que pour entier naturel n\geq2 \sum_{i=2}^n i*2^i=2^{n+1}(n-1) j'ai commencé à faire par : soit Pn " \sum_{i=2}^n i*2^i=2^{n+1}(n-1) " Initialisation : n_0=2 \sum_{i=2}^2 2*2^2=8 2^{2+1}(2-1)=8 donc P_0 est vraie Hérédité : ...
- par Raph1
- 01 Nov 2013, 11:45
-
- Forum: ✯✎ Supérieur
- Sujet: raisonnement par récurrence
- Réponses: 16
- Vues: 602
chan79 a écrit:non, si tu prends 11pi/6, ça marche
ah je crois j'ai compris

- par Raph1
- 30 Oct 2013, 14:46
-
- Forum: ✯✎ Supérieur
- Sujet: trigonométrie
- Réponses: 20
- Vues: 710
chan79 a écrit:non, 3pi/2, par exemple, n'est pas solution
on visualise les solutions sur le cercle trigonométrique
donc les solutions c'est juste

?
- par Raph1
- 30 Oct 2013, 14:33
-
- Forum: ✯✎ Supérieur
- Sujet: trigonométrie
- Réponses: 20
- Vues: 710
non ca peut être sa, je me suis tromper je pense parce que c'est [0,2pi]
- par Raph1
- 30 Oct 2013, 14:04
-
- Forum: ✯✎ Supérieur
- Sujet: trigonométrie
- Réponses: 20
- Vues: 710
chan79 a écrit:c'est bien parti
après ca fait x=pi ou x=pi/3 et donc tableau de signe je pense que les solutions sont

ou c'est pas du tout sa ?
- par Raph1
- 30 Oct 2013, 14:02
-
- Forum: ✯✎ Supérieur
- Sujet: trigonométrie
- Réponses: 20
- Vues: 710
j'ai fais le discriminant et les 2 solutions, j'arrive à
cos x = -1 ou cos x = 1/2 (pour les 2 solutions quand l'équation est égale à 0)
- par Raph1
- 30 Oct 2013, 13:51
-
- Forum: ✯✎ Supérieur
- Sujet: trigonométrie
- Réponses: 20
- Vues: 710
oui je sais résoudre sa, delta, on trouve les solutions, tableau de signe et on regarde quand c'est supérieur a 0
- par Raph1
- 30 Oct 2013, 13:33
-
- Forum: ✯✎ Supérieur
- Sujet: trigonométrie
- Réponses: 20
- Vues: 710
chan79 a écrit:salut
cos(2x)=2cos²x-1
ça peut peut-être aider
j'avais déjà fais sa oui mais je vois pas après
- par Raph1
- 30 Oct 2013, 13:15
-
- Forum: ✯✎ Supérieur
- Sujet: trigonométrie
- Réponses: 20
- Vues: 710
salut,
je dois résoudre dans
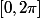
, l'équation
+\cos(x)\geq0)
j'ai commencé quelque chose mais je ne pense pas que c'est sa, j'ai juste besoin du début je pense qu'après je saurai finir
- par Raph1
- 30 Oct 2013, 13:07
-
- Forum: ✯✎ Supérieur
- Sujet: trigonométrie
- Réponses: 20
- Vues: 710
par
par