Oui, c'est vrai, je me suis trompé.
Bien sûr, c'est le zéro là.
(je vais éditer)
11 résultats trouvés
Revenir à la recherche avancée
- 28 Nov 2012, 21:41
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] Isomorphisme entre groupes et pgcd
- Réponses: 11
- Vues: 1045
Mais bon, maintenant, je crois que j'ai réussi. Si je prendre un isomorphisme \phi de mnZ dans \frac{Z}{mZ} X \frac{Z}{nZ} , et d = pgcd (m, n), alors, \phi (1) c'est un générateur de \frac{Z}{mZ} X \frac{Z}{nZ} , correct? Alors, l'ordre de \phi (1) = mn (car, ça c'est l'ordre de mnZ...
- 28 Nov 2012, 20:59
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] Isomorphisme entre groupes et pgcd
- Réponses: 11
- Vues: 1045
- 28 Nov 2012, 20:50
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] Isomorphisme entre groupes et pgcd
- Réponses: 11
- Vues: 1045
leon1789, si pgdc (m, n) = 1, alors, je peux construire un isomorphisme entre eux. (En fait, j'ai fait ça pour montrer l'implication dans l'autre sens). Mais, maintenant, si je suppose que il y a un isomorphisme, je ne sais pas montrer que pgcd (m, n) = 1. Bon, je vais voir les pistes que vous et L....
- 28 Nov 2012, 20:39
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] Isomorphisme entre groupes et pgcd
- Réponses: 11
- Vues: 1045
[TERMINÉ] Isomorphisme entre groupes et pgcd
Quelqu'un ici a une idée de comment montrer que
s'il existe un isomorphisme de dans
dans  ,
,
alors, = 1)
?
* m et n sont nombres entiers plus grand que 0
* c'est le produit cartésien.
c'est le produit cartésien.
Merci beacoup!
s'il existe un isomorphisme de
alors,
?
* m et n sont nombres entiers plus grand que 0
*
Merci beacoup!
- 28 Nov 2012, 10:47
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] Isomorphisme entre groupes et pgcd
- Réponses: 11
- Vues: 1045
- 27 Nov 2012, 15:35
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] si l'intersection de mZ avec nZ égal mnZ, alors pg
- Réponses: 8
- Vues: 991
- 27 Nov 2012, 15:21
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] si l'intersection de mZ avec nZ égal mnZ, alors pg
- Réponses: 8
- Vues: 991
- 27 Nov 2012, 15:14
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] si l'intersection de mZ avec nZ égal mnZ, alors pg
- Réponses: 8
- Vues: 991
- 27 Nov 2012, 15:09
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] si l'intersection de mZ avec nZ égal mnZ, alors pg
- Réponses: 8
- Vues: 991
- 27 Nov 2012, 15:08
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] si l'intersection de mZ avec nZ égal mnZ, alors pg
- Réponses: 8
- Vues: 991
[TERMINÉ] si l'intersection de mZ avec nZ égal mnZ, alors pg
Je voudrais bien montrer que
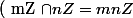 \Rightarrow pgcd (m, n) = 1$)
Quelque idée?
Merci bcp.
Quelque idée?
Merci bcp.
- 27 Nov 2012, 14:53
- Forum: ✯✎ Supérieur
- Sujet: [TERMINÉ] si l'intersection de mZ avec nZ égal mnZ, alors pg
- Réponses: 8
- Vues: 991
- 11 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
