Forum de Mathématiques: Maths-Forum

adamNIDO a écrit:remarque

on peut trouve même résultât sans passer par la formule d'ito parce que comme vous le savez que un mouvement bronian est un processus gaussien donc on peut facilement calculer espérance de

Effectivement j'arrive à ce résultat là. Encore merci pour votre aide. Bonne journée! :we:

Je n'avais pas vu votre message du dessus, on tombe bien sur le même résultat intermédiaire, je vais essayer de le dépatouiller!

Merci encore pour votre aide précieuse. C'est génial!

:we:

adamNIDO a écrit:applique la formule d'ito a cela vous donne

J'ai beau utiliser la formule d'Itô je ne retrouve pas votre résultat :



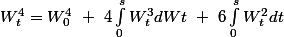
J'arrive à ça en utilisant la formule dans mon cours...

Ah oui pardon, j'étais arrivé à ça aussi par fubini, c'est après que je bloque.

Je ne vois pas comment calculer l'espérance d'une variable à la puissance 4.
Peut-être avec la formule de Koenig?

Ça me paraît un peu laborieux!

D'après moi, on peut choisir a et b en posant

et

Je suis donc arrivé à l'espérance suivante :



Mais je suis bloqué pour la calculer...

est ce que vous avez fait la notion de crochet d'une martingale Bonjour et merci encore pour vos réponses! Je n'ai pas encore vu la notion de crochet pour une matingale. Je suis arrivé, en posant E[\int_{0}^T (W_u^2 1_{u \leq t})(W_u^2 1_{u \leq s})dW_u] = E[\int_{0}^T W_u^4 1_{u \l...

Bonjour à toutes et à tous! Voilà je vous expose mon problème. J'ai une question sur un exo sur laquelle je bute. L'exercice proposé contient trois questions, j'ai répondu aux deux premières mais je bloque sur la dernière. Voici pour vous remettre dans le contexte : On considère un mouvement brownie...

Si tu veux une fonction continue partout sauf en 0 tu peux prendre par exemple sin(1/x)!

Bonjour!
pour ta question 2 ce n'est pas plutôt une fonction continue partout sauf en 0? Parce que une fonction continue seulement en 0, je ne vois pas trop à part le point 0 lui-même!