13 résultats trouvés
Revenir à la recherche avancée
Z=\frac{3x^2+3y^2-5x-2 + i(-7y)}{(x-2)^2 + y^2} Ce n'est pas puisque Z est réel, on a Z=\bar Z mais : une condition nécessaire et suffisante pour que Z soit réel est que Z=\bar Z soit \frac{3z+1}{z-2} = \frac{3\bar z+1}{\bar z-2} (3z+1)(\bar z-2)-(3\bar z+1)&...
- par Alexandrat22
- 03 Déc 2012, 21:07
-
- Forum: ✎✎ Lycée
- Sujet: Nombres complexes
- Réponses: 3
- Vues: 7484
Bonjour, j'ai un exercice à résoudre mais je n'arrive pas très bien. Merci de m'aider. Soit z \in \mathbb{C} - {2} et Z= \frac{3z+1}{z-2} Le but de l'exercice est de déterminer l'ensemble E des nombres complexes z pour lequel Z est un nombre réel. 1. Avec les parties réelle et imaginaire a. On pose ...
- par Alexandrat22
- 03 Déc 2012, 19:53
-
- Forum: ✎✎ Lycée
- Sujet: Nombres complexes
- Réponses: 3
- Vues: 7484
sylvainp a écrit:Non tu ne peux pas aller plus loin, et le résultat est plutôt lisible comme ça.
D'accord, merci beaucoup de votre aide
- par Alexandrat22
- 11 Nov 2012, 20:42
-
- Forum: ✎✎ Lycée
- Sujet: Dérivée
- Réponses: 17
- Vues: 687
l'erreur est dans le calcul de -(x(exp(-x))*2x ça fait pas -3x*exp(-x) mais -2x²*exp(-x) tu retrouves le résultats que j'ai écrit un peu avant Ah oui d'accord. Et une fois factorisée, on obtient \frac{e^-^x(1-x-x^2-x^3)}{(x^2+1)^2} mais le calcul n'est pas fini là ? Je ne voie pas s...
- par Alexandrat22
- 11 Nov 2012, 20:21
-
- Forum: ✎✎ Lycée
- Sujet: Dérivée
- Réponses: 17
- Vues: 687
Est-ce qu'en développent en obtient : f'(x) = \frac{x^2e^-^x+e^-^x-x^3e^-^x-xe^-^x-3xe^-^x}{(x^2+1)^2} ? Lorsque je factorise par e^-^x avec le développement que j'ai fais au dessus, j'obtiens pour le numérateur : e^-^x(x^2+1-x^3-x-3x) J'ai du faire une erreur mais je ne voie pas où.
- par Alexandrat22
- 11 Nov 2012, 20:03
-
- Forum: ✎✎ Lycée
- Sujet: Dérivée
- Réponses: 17
- Vues: 687
Alexandrat22 a écrit:Par contre je ne sais pas trop comment m'y prendre pour développer
Est-ce qu'en développent en obtient :
f'(x) =
^2})
?
- par Alexandrat22
- 11 Nov 2012, 19:43
-
- Forum: ✎✎ Lycée
- Sujet: Dérivée
- Réponses: 17
- Vues: 687
sylvainp a écrit:Ouais parfait!
Par contre je ne sais pas trop comment m'y prendre pour développer
- par Alexandrat22
- 11 Nov 2012, 19:22
-
- Forum: ✎✎ Lycée
- Sujet: Dérivée
- Réponses: 17
- Vues: 687
Il reste une petite erreur dans le calcul de u'=U'V+V'U U'=1 V=exp(-x) U=x V'=-exp(-x) donc u'=exp(-x)-x*exp(-x) et non pas u'=x comme tu trouves Ah oui j'ai fais une erreur. Du coup on à : f'(x)= \frac{((e^-^x-x*e^-^x)(x^2+1))-((x*e^-^x)2x)}{(x^2+1)^...
- par Alexandrat22
- 11 Nov 2012, 19:16
-
- Forum: ✎✎ Lycée
- Sujet: Dérivée
- Réponses: 17
- Vues: 687
Attention, comme tu l'avais dit dans ton premier message, ta fonction est de la forme u/v ! ton raisonnement pour calculer la dérivée d'un quotient était donc correct : (u/v)'= (u'v-v'u)/v². Par contre, c'est un peu compliqué car u au numérateur est un produit de fonction u=U*V, donc la dérivée u' ...
- par Alexandrat22
- 11 Nov 2012, 19:04
-
- Forum: ✎✎ Lycée
- Sujet: Dérivée
- Réponses: 17
- Vues: 687
J'obtiens donc

=
}{x^2+1})
=

Ensuite est-ce que je met cette fraction sous la forme
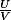
?
- par Alexandrat22
- 11 Nov 2012, 18:26
-
- Forum: ✎✎ Lycée
- Sujet: Dérivée
- Réponses: 17
- Vues: 687
Ok je vais donc essayer de refaire la dérivée avec cet élément. Merci
- par Alexandrat22
- 11 Nov 2012, 18:10
-
- Forum: ✎✎ Lycée
- Sujet: Dérivée
- Réponses: 17
- Vues: 687
Bonjour. J'ai une fonction f à dérivée, mais je n'y arrive pas. Soit f la fonction définie sur [0 ; +00[ par : \frac{xe^-^x}{x^2+1} Je vois que c'est de la forme \frac{u}{v} avec u= xe^-^x et u'= {-}e^{-x} v= x^2+1 et v'= 2x On à donc f'(x) = \frac {-e^-^x(x^2+1)-xe^{-x}(2x)}{(x^...
- par Alexandrat22
- 11 Nov 2012, 17:59
-
- Forum: ✎✎ Lycée
- Sujet: Dérivée
- Réponses: 17
- Vues: 687
