7 résultats trouvés
Revenir à la recherche avancée
- 12 Nov 2012, 17:43
- Forum: ✎✎ Lycée
- Sujet: Nombre complexe
- Réponses: 10
- Vues: 667
- 11 Nov 2012, 23:10
- Forum: ✎✎ Lycée
- Sujet: Nombre complexe
- Réponses: 10
- Vues: 667
J'ai refait les calcul. Pour z'=(2+i)x^2+iy^2+4i(i-1)x+2i+2 Je trouve : z' = 2x^2-4x+2+i(x^2+y^2-4x+2) Re(z')=2x^2-4x+2 Im(z')=x^2+y^2-4x+2 1. z' appartient à R \Longleftrightarrow Im(z')=0 \Longleftrightarrow x^2+y^2-4x+2=0 A parti...
- 11 Nov 2012, 12:22
- Forum: ✎✎ Lycée
- Sujet: Nombre complexe
- Réponses: 10
- Vues: 667
- 10 Nov 2012, 22:59
- Forum: ✎✎ Lycée
- Sujet: Nombre complexe
- Réponses: 10
- Vues: 667
Pour la 1er question :
A partir de ça ->)
=2x^2-4x+2)
z' est réel si et seulement si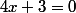
Pour la deuxième :
=4x+3)
z' est imaginaire pur si et seulement si
A partir de ça ->
z' est réel si et seulement si
Pour la deuxième :
z' est imaginaire pur si et seulement si
- 10 Nov 2012, 22:19
- Forum: ✎✎ Lycée
- Sujet: Nombre complexe
- Réponses: 10
- Vues: 667
D'accord. Mais comment je fais pour prouver que Im(z')=0 et Re(z')=0 dans les deux première questions ?
- 10 Nov 2012, 22:00
- Forum: ✎✎ Lycée
- Sujet: Nombre complexe
- Réponses: 10
- Vues: 667
Nombre complexe
Bonjour, J'ai un problème face au dernier exercice de mon devoir maison. Voici l'énoncé : On considère le nombre complexe z'=(2+i)x^2+iy^2+4i(i-1)x+2i+2 , où x et y sont 2 nombres réels. 1. Déterminer l'ensemble E1 des points M du plan de coordonnées (x;y) tels que z' est réel. 2...
- 10 Nov 2012, 21:56
- Forum: ✎✎ Lycée
- Sujet: Nombre complexe
- Réponses: 10
- Vues: 667
- 7 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
