Forum de Mathématiques: Maths-Forum

Que veux-tu dire par définition ? Veux-tu dire quelque chose comme ça (x,y) \in R \Leftrightarrow x \leq y , par exemple ? Si oui, je dirais dans ce cas que R n'est pas défini. Puisque, d'après moi, il faut seulement jouer avec la propriété de transitivité ici. Si non, est-ce quelque chose q...

Bonjour à tous! Voici l'exercice que j'ai à faire: Si la relation R sur X est transitive, démontrez que la relation R \circ R l'est aussi. Posons: p: (x,y) \in R \wedge (y,z) \in R \Rightarrow (x,z) \in R q: (x,y) \in R \circ R \wedge (y,z) \in R \circ R \Righ...

Tu as raison!

Ce qui fait que et donc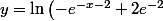

Ce qui est confirmé par le solutionnaire détaillé. (Je je comprends toujours pas la réponse donnée par mon enseignante...).

Merci!

Mathieu

J'ai un exercice à faire, on peut y lire : Résolver l'équation différentielle suivante en tenant compte de la condition initiale indiquée. 1. \frac{dy}{dx}=e^{-x-y-2} (Condition : y(0) = -2 ) 2. dy=e^{-x-2} *e^{-y} *dx 3. \int \frac{dy}{e^{-y} }=\int e^{-x-2} *dx 4. [-e^{-y} =-e^{-x-2} +C_{1} ] (Mis...