Forum de Mathématiques: Maths-Forum

??

C'est a dire que c'est ma premiere serie plus la seconde ie
avec et

Et avec ce rayon de convergence, il me faut en faire quoi a present ?

mmmm je m'en sors pas du rayon de convergence tout d'un bloc... j'essaye de resoudre u_n_+_1 / u_n mais ca me conduit a rien que je sache reduire Voyons voir, puis-je ecrire : (5.2^n -1)/(5.2^{n-1}-1) = (5.2^{n-1}-1)/(5.2^{n-1}-1) + 5.2/(5.2^{n-1}-1) = 1 + &#...

mmmm je m'en sors pas du rayon de convergence tout d'un bloc... j'essaye de resoudre mais ca me conduit a rien que je sache reduire

aaaah s'eut été trop facile... et du coup pas si simple le rayon de convergence...

En fait je l'ai compris partiellement : mes ryons de convergences des deux series sont ils bons ? 1/2 et 1 ? Dans le cas positif, que dois je faire ensuite de ces deux rayons et de ces deux series ?

@doniram]non OK je crois que j'ai compris : tu recherches l'expression de la fonction f telle que \bigsum_{k=0}^{+ \infty} a_k x^k=f(x) \in\mathbb{R} avec x qui appartient au disque de convergence de cette série entière Merci de confirmer (ou de me dire que j'ai rien compris) A+ OUIIII c'es...

Je trouve pour ma première suite un rayon de convergence de 1/2 et pour la suite un rayon de convergence de 1 . Je dois revoir mes calculs ou bien je peux continuer ?

non, en fait mon problème semble plus simple, tout simplement je cherche la démarche pour transformer cette somme en fonction f(x)
D’après ce que j'entrevois, je dois chercher le rayon de convergence de mes deux séries et définir leur somme... Est ce bien cela ?

Bonjour, j'arrive a me debrouiller de la suite
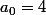définie par avec j'ai = non, mon problème est pour transformer cette somme en une fonction f(x) ne dépendant que de x...

Voila, quelqu'un pourrait il m'indiquer le process a suivre pour calculer ce genre de somme de series : Somme de k=0 a infini de An.X^n avec An= 2A(n-1) +1 et A0 = 4 Bon je sais me dépatouiller de la suite arithmético-géométrique et exprimer An en fonction de n. C'est pour le reste que je n'ai pas d...

Bon bon bon, du coup, j'ai Somme(1 a inf) a(n-1)X^n + 2a(2) + Somme(1 a inf) (n+1)(n+2)a(n+2)X^n =0 Ce qui donne 2a2=0 & a(n+2) = a(n-1)/(n+1)(n+2) (obligé n'est ce pas le 2a2= 0 n'est ce pas?) D'ou a(3k)= ao/Produit(p=0 a k) 3p.(3p-1) a(3k+1) = a1/Produit(p=0 a k) 3p.(3p+1) a(3k+2) = a2/Produit...

Cependant je reste avec un problème... Les coefficients ne s'annulent pas... Mais sinon, oui oui c'est cela que je cherche je me retrouve avec X.Somme (de n=o, a inf) anX^n + Somme (de n=2, a inf) de n(n-1)an.X^n-2 Ce qui donne : Somme (de n=o, a inf) anX^n+1 + (n+2)(n+1)an+2.X^n et c'est ce dernier...

Une question, a quoi correspond sur Wolfram Ai et Bi ? je n'arrive pas a saisir...

Bon, y a t'il une méthodologie appropriée?

Aaaaah ben merci, je jette un coup d'oeil

Bonjour amis matheux?

Que pensez vous de cette equation?

Y" +XY = 0

Quand j'essaye par les DL, je me retrouve avec un X^n+1 dont je ne sais pas me debarrasser...
Quelle est la methode a utiliser?
Merci